AnglePath

AnglePath[{θ1,θ2,θ3,…}]

gives the list of 2D coordinates corresponding to a path that starts at {0,0}, then takes a series of steps of unit length at successive relative angles θi.

AnglePath[{{r1,θ1},{r2,θ2},{r3,θ3},…}]

takes successive steps of lengths ri.

AnglePath[θ0,{step1,step2,…}]

starts at angle θ0 with respect to the axis.

AnglePath[{x,y},{step1,step2,…}]

starts at the point {x,y} with initial angle 0 with respect to the axis.

AnglePath[{{x,y},θ0},{step1,step2,…}]

starts at {x,y} with initial angle θ0 with respect to the axis.

AnglePath[{{x,y},{dx,dy}},{step1,step2,…}]

takes the first step to go from {x,y} to {x+dx,y+dy}.

AnglePath[init,steps,form]

returns at each step the data of the form specified by form.

Details and Options

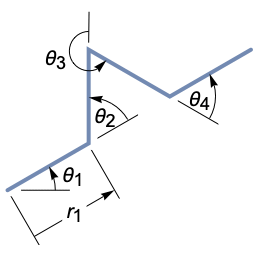
  • At each point reached in the formation of a path, AnglePath in effect first rotates by the specified relative angle, then advances by the specified distance.
  • Unless explicitly given as Quantity objects, the angles θi are assumed to be in radians, increasing counterclockwise. (Multiply by Degree to convert from degrees.)
  • In AnglePath[{θ1,θ2,θ3,…}], the angle θ1 is assumed to be relative to the 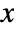axis.
  • Possible choices for form in AnglePath[…,form] include:
  • "Position"Cartesian coordinates {xi,yi} (default)
    "FrameMatrix"rotation matrix of the current frame with respect to the initial frame
    "RelativeMatrix"rotation matrix of the current frame with respect to the previous frame
    "FrameAngle"rotation angle with respect to the initial step
    "RelativeAngle"rotation angle with respect to the previous step
    "Translation"translation transformation from the initial step
    "Rotation"rotation transformation from the initial step
    "RotationTranslation"rotation-translation transformation from the initial step
    {form1,form2,…}list of forms
  • The arguments of AnglePath can be symbolic. They can also be Quantity objects.
  • AnglePath has the option WorkingPrecision, which determines the precision of numbers generated.
  • With the default setting WorkingPrecisionAutomatic, exact numbers will be generated for exact input only for fairly short paths; for longer paths, machine precision will be used.

Examples

open allclose all

Basic Examples  (5)

Starting at {0,0} along the axis, move several unit steps, rotating 90° before each step:

A polyline of three segments:

Advance 20 steps, always turning 110° toward the left:

Generate the transformation functions of a path:

Apply them to a turtle:

Use symbolic input:

Scope  (13)

Steps Specification  (3)

Advance in unit steps of specified successive angles, starting from the axis:

Specify the lengths of the steps:

Use Quantity objects in input:

Path Initialization  (4)

Specify the initial position:

Specify the initial orientation:

Specify both the initial position and orientation:

Use a Cartesian {dx,dy} specification for the initial orientation:

Forms of Output  (6)

By default, AnglePath returns the position reached at each step:

Compute the orientation of each local frame with respect to the previous local frame:

Compute the orientation of each local frame with respect to the global frame:

Compute the angle determining the orientation of each local frame in the global frame:

Generate rotation-translation transformations from the initial step:

Apply them to a triangle:

Produce different types of output with one AnglePath call:

The first elements of the triples are the rotation matrices with respect to the previous frame:

The second elements are the positions:

The third elements are the transformation functions from the initial frame:

Options  (1)

WorkingPrecision  (1)

By default, AnglePath with exact input gives exact numbers for short paths and machine numbers for long paths:

Specify infinite working precision to perform exact, but slower computations:

Use any specified precision for the computations:

Applications  (3)

Make a random walk where successive steps change direction by at most 20°:

Generate a dragon curve:

Generate a Koch snowflake curve:

Another pattern based on the Thue–Morse sequence:

Properties & Relations  (5)

Angles are accumulated in subsequent steps, starting with θ0:

These two results are identical:

Take 100 random angles between and :

Considered as absolute angles, they represent on average a collection of steps toward the right:

Considered as relative angles, the path may evolve in any possible direction. The total length is the same:

Global frame rotations can be obtained as multiplications of all previous relative rotations:

Compute the positions for a path with the following inputs:

Each new position can be computed as a displacement along a rotation of the initial x axis:

Possible Issues  (1)

When using the notation {{x,y},{dx,dy}} for the first argument, {dx,dy} determines the initial orientation, not the position of the next point:

Interactive Examples  (1)

Move the turtle by steps of given length and relative direction:

Neat Examples  (4)

Draw lines for which each segment forms a uniformly increasing angle with the previous segment:

Draw lines for which consecutive relative angles increase by 1 radian:

Draw a line for which consecutive relative angles increase and are modulated by a Sin function:

Add color to the individual segments of the angle path:

Wolfram Research (2015), AnglePath, Wolfram Language function, https://reference.wolfram.com/language/ref/AnglePath.html (updated 2019).

Text

Wolfram Research (2015), AnglePath, Wolfram Language function, https://reference.wolfram.com/language/ref/AnglePath.html (updated 2019).

CMS

Wolfram Language. 2015. "AnglePath." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/AnglePath.html.

APA

Wolfram Language. (2015). AnglePath. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AnglePath.html

BibTeX

@misc{reference.wolfram_2024_anglepath, author="Wolfram Research", title="{AnglePath}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/AnglePath.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_anglepath, organization={Wolfram Research}, title={AnglePath}, year={2019}, url={https://reference.wolfram.com/language/ref/AnglePath.html}, note=[Accessed: 18-December-2024 ]}