BUILT-IN WOLFRAM LANGUAGE SYMBOL

GeometricTransformation

GeometricTransformation[g,tfun]
represents the result of applying the transformation function tfun to the geometric objects corresponding to the primitives g.

GeometricTransformation[g,m]
transforms geometric objects in g by effectively replacing every point r by m.r.

GeometricTransformation[g,{m,v}]
effectively replaces every point r by m.r+v.

GeometricTransformation[g,{t₁,t₂,…}]
represents multiple copies of g transformed by a collection of transformations.

Details and Options Details and Options

GeometricTransformation[g,…] remains unchanged under evaluation, but affects how g is rendered.
GeometricTransformation works on lists of graphics primitives and directives in 2D and 3D.
GeometricTransformation[g,{m,v}] effectively applies an affine transform to g.
GeometricTransformation[g,{{m_xx,m_yx},{m_xy,m_yy}}] transforms the unit vectors 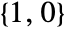and 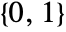to {m_xx,m_xy} and {m_yx,m_yy}, respectively.
For different spec, GeometricTransformation[g,{m,spec}] leaves fixed the following special points on the bounding box of g:

	Center	center
	Left	midpoint of the left side
	Right	midpoint of the right side
	Top	midpoint of the top
	Bottom	midpoint of the bottom
	Front	midpoint of the front
	Back	midpoint of the back
	{Left,Top}, etc.	corners

For objects specified with scaled coordinates Scaled[{x,y}], GeometricTransformation effectively applies its transformation to the corresponding ordinary coordinates.
Normal[expr] if possible replaces all GeometricTransformation[g_i,…] constructs by versions of the g_i in which the coordinates have explicitly been transformed.
The following option can be given:
ContentSelectable Automatic whether to allow contents to be selected
For matrices m₁ and m₂, GeometricTransformation[GeometricTransformation[g,m₁],m₂] is equivalent to GeometricTransformation[g,m₂.m₁].