ImageTransformation[image,f]
gives an image in which each pixel at position p corresponds to the position f[p] in image.
ImageTransformation[image,f,size]
gives an image of the specified size.
ImageTransformation[video,…]
transforms frames of a video.


ImageTransformation
ImageTransformation[image,f]
gives an image in which each pixel at position p corresponds to the position f[p] in image.
ImageTransformation[image,f,size]
gives an image of the specified size.
ImageTransformation[video,…]
transforms frames of a video.
Details and Options




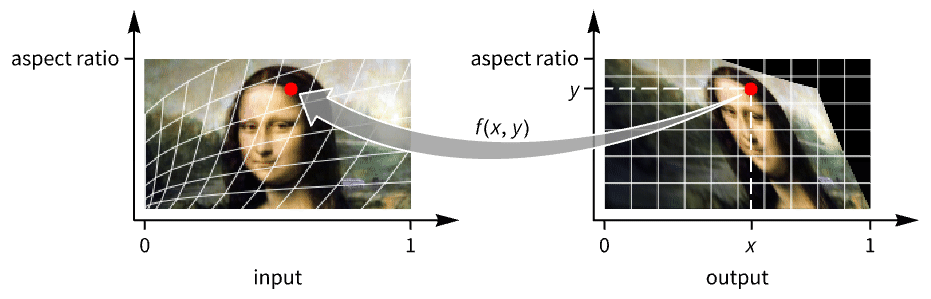
- ImageTransformation[image,f] is also known as backward transformation, where the value of every pixel at position {x,y} in the output image is obtained from the position f[{x,y}] in the input image.
- The transformation function f can be one of the following:
-
f an arbitrary function f TransformationFunction[…] a transformation function - For video inputs, the transformation function can also be a function of time (in seconds from the start). The function returns a frame in which each pixel at time t and position p corresponds to the position f[t][p].
- ImageTransformation works with arbitrary 2D and 3D images.
- Possible settings for size are:
-
Automatic automatic image size All same as input image size width explicit width, automatic height {width,height} explicit width and height {width,depth,height} explicit width, depth and height in 3D - For possible width, depth and height specifications, see the reference page for ImageResize.
- In 2D, the range of the coordinate system for the input image is assumed to be
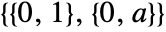 , where
, where 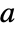 is the aspect ratio. The bottom-left corner of the image corresponds to coordinates
is the aspect ratio. The bottom-left corner of the image corresponds to coordinates 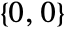 by default.
by default. - In 3D, the range of the coordinate system for the input image is assumed to be
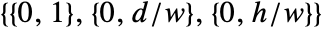 , where
, where 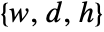 are the image dimensions. The bottom-left front corner of the image corresponds to coordinates
are the image dimensions. The bottom-left front corner of the image corresponds to coordinates 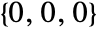 by default.
by default. - Other coordinate systems can be specified by setting the DataRange option.
- ImageTransformation can take the following options:
-
Background 0 background color to use DataRange Automatic range of coordinates in the original image Masking Full region of interest to be transformed Padding 0 padding method PlotRange Automatic range of coordinates in the resulting image Resampling Automatic resampling method - By default, ImageTransformation returns an image with the aspect ratio of the input image.
- Typical settings for DataRange include:
-
Automatic 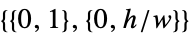 in 2D,
in 2D, 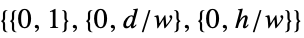 in 3D
in 3DFull 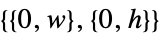 in 2D,
in 2D, 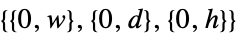 in 3D
in 3D{{left,right},{bottom,top}} explicit coordinate ranges in 2D {{left,right},{front,back},{bottom,top}} explicit coordinate ranges in 3D - The coordinate system of the resulting image is specified by the PlotRange option. Typical settings include:
-
Automatic same as DataRange settings All try to include all of the transformed pixels Full same ranges as the input image {{left,right},…} explicit coordinate ranges - In ImageTransformation[image,f], the pixel dimensions of the resulting image are based on the dimensions of image and the ratio of PlotRange and DataRange.
- The Masking option can be one of the following:
-
All input image only Full input image and padding mask any mask image
Examples
open all close allScope (13)
Data (4)
Transformation (7)
Use any function for the transformation:
Operate explicitly on ![]() and
and ![]() pixel positions:
pixel positions:
Operate on the vertical dimension only:
Perform a matrix transformation:
Use a TransformationFunction to specify the transformation:
Transform frames of a video as a function of time and position:
Size (2)
By default, the output image is of the same size as the input image:
Specify the size of the resulting image:
Specify width and height explicitly:
Use All to obtain an image of the same size as the original:
Options (7)
Background (1)
DataRange (2)
Masking (1)
By default, Masking->Full is used; padding is used for pixels outside of the original image:
With Masking->All, the Background option value is used for pixels outside of the original image:
PlotRange (1)
Padding (1)
By default, Padding0 is used:
Applications (6)
Properties & Relations (2)
History
Introduced in 2010 (8.0) | Updated in 2014 (10.0) ▪ 2020 (12.1) ▪ 2021 (13.0)
Text
Wolfram Research (2010), ImageTransformation, Wolfram Language function, https://reference.wolfram.com/language/ref/ImageTransformation.html (updated 2021).
CMS
Wolfram Language. 2010. "ImageTransformation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ImageTransformation.html.
APA
Wolfram Language. (2010). ImageTransformation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImageTransformation.html
BibTeX
@misc{reference.wolfram_2025_imagetransformation, author="Wolfram Research", title="{ImageTransformation}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ImageTransformation.html}", note=[Accessed: 13-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_imagetransformation, organization={Wolfram Research}, title={ImageTransformation}, year={2021}, url={https://reference.wolfram.com/language/ref/ImageTransformation.html}, note=[Accessed: 13-March-2026]}