WOLFRAM

Wolfram Language & System Documentation Center

TransformationFunction[data]

represents a transformation function that applies geometric and other transformations.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Constructing TransformationFunction  
Working with TransformationFunction as a Function  
Working with TransformationFunction as a Formula  
Applications  
Properties & Relations  
See Also
Related Guides
History
Cite this Page

TransformationFunction

TransformationFunction[data]

represents a transformation function that applies geometric and other transformations.

Details

  • TransformationFunction[…] objects are generated by constructors such as TranslationTransform, RotationTransform, etc.
  • TransformationFunction[…][x] applies the transformation function to a vector x, returning a transformed vector.
  • TransformationFunction[…][{x1,x2,…}] for a list of vectors applies the transformation to each vector xi, producing a list of transformed vectors.
  • TransformationFunction works with both numerical and symbolic vectors and represents a linear fractional transformation 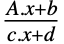, where A∈Matrices[{m,n}], b∈Matrices[{m,1}], c∈Matrices[{1,n}] and d∈Matrices[{1,1}].
  • For smaller dimensions, it is typically displayed as an 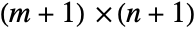transformation matrix 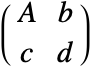. TransformationMatrix can be used to extract the transformation matrix.
  • Composition[t1,t2] where ti has transformation matrix 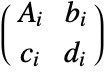gives a new TransformationFunction object with transformation matrix .
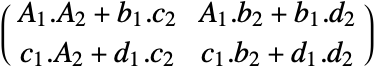  • InverseFunction[t] where t has transformation matrix 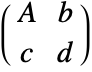gives a new TransformationFunction object with transformation matrix 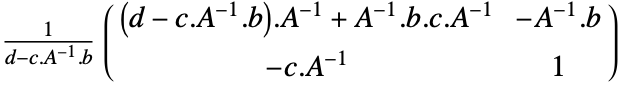where 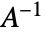is the matrix inverse.
  • GeometricTransformation can be used to represent the effect of applying a TransformationFunction object to geometrical or graphics objects when restricted to affine transformations.
  • TransformationFunction[…][prop] gives the transformation property prop. For a transformation function with transformation matrix 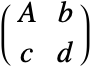, properties include:
  • "AffineQ"whether the transformation is structurally affine or not, it gives True if both c and d are zero
    "AffineMatrix"the matrix A
    "AffineVector"the vector b
    "FractionalVector"the vector c
    "FractionalConstant"the constant d
    "ArgumentLength"the length n of the vector x
    "ResultLength"the length m of the result vector
    "TransformationMatrix"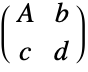

Examples

open all close all

Basic Examples  (1)

Create a rotation transform:

This rotates the vector {x,y} by angle θ:

Scope  (15)

Constructing TransformationFunction  (10)

A translation by the vector {qx,qy,qz}:

A rotation around the axis:

Scaling along the coordinate axes:

Shearing in the direction by an angle θ:

Reflecting in the plane:

Rescaling the box [xmin, xmax][ymin, ymax] to the unit square:

A general TransformationFunction:

A linear transformation:

An affine transformation:

A linear fractional transformation:

Working with TransformationFunction as a Function  (4)

Here is a rotation of around the axis:

This transforms the axis:

This transforms a list of vectors:

Composing two transformations:

Computing the inverse:

This shows they are inverses:

Computing the partial derivative :

Working with TransformationFunction as a Formula  (1)

This defines a general transform:

This is the corresponding formula:

A derivative:

A limit:

An integral:

A plot:

Applications  (2)

TransformationFunction can be used as an argument to GeometricTransformation:

Integrate a function over a rhombic region:

defines a change of variables that maps the unit square to the integration region:

The integrand in the new coordinates:

The Jacobian:

Properties & Relations  (1)

Find the ^(th) power of a transformation:

Apply t five times:

Apply tt[5]:

Find the ^(th) iteration using RSolve:

Wolfram Research (2007), TransformationFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/TransformationFunction.html (updated 2019).

Text

Wolfram Research (2007), TransformationFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/TransformationFunction.html (updated 2019).

CMS

Wolfram Language. 2007. "TransformationFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/TransformationFunction.html.

APA

Wolfram Language. (2007). TransformationFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransformationFunction.html

BibTeX

@misc{reference.wolfram_2025_transformationfunction, author="Wolfram Research", title="{TransformationFunction}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/TransformationFunction.html}", note=[Accessed: 30-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_transformationfunction, organization={Wolfram Research}, title={TransformationFunction}, year={2019}, url={https://reference.wolfram.com/language/ref/TransformationFunction.html}, note=[Accessed: 30-October-2025]}