Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

RotationTransform

RotationTransform[θ]

gives a TransformationFunction that represents a rotation in 2D by θ radians about the origin.

RotationTransform[θ,p]

gives a 2D rotation about the 2D point p.

RotationTransform[θ,w]

gives a 3D rotation around the direction of the 3D vector w.

RotationTransform[θ,w,p]

gives a 3D rotation around the axis w anchored at the point p.

RotationTransform[{u,v}]

gives a rotation about the origin that transforms the vector u to the direction of the vector v.

RotationTransform[{u,v},p]

gives a rotation about the point p that transforms u to the direction of v.

RotationTransform[θ,{u,v},…]

gives a rotation by θ radians in the plane spanned by u and v.

Details

RotationTransform gives a TransformationFunction that can be applied to vectors.
θ Degree or θ° specifies an angle in degrees.
RotationTransform[θ,{u,v},p] can be used to specify any rotation about any point p, in any number of dimensions.
Positive θ in RotationTransform[θ,{u,v},p] corresponds to going from the direction of u toward the direction of v.
RotationTransform[θ] is equivalent to RotationTransform[θ,{{1,0},{0,1}}].
RotationTransform[θ,w] is equivalent to RotationTransform[θ,{u,v}], where u⊥w, v⊥w, and u,v,w form a right-handed coordinate system.
RotationTransform[θ,{u,v}] can effectively specify any element of the 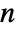-dimensional rotation group 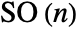. RotationTransform[θ,{u,v},p] can effectively specify any element of the 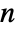-dimensional special Euclidean group.

Examples

open allclose all

Basic Examples (4)

A 2D rotation transform by θ radians:

Rotate a vector:

Rotate around the axis:

Rotate a 2D graphic by 30° about the origin:

Rotate around the axis:

Scope (9)

Rotation by θ radians about the point {px,py}:

Rotation by θ radians around the axis about the point {px,py,pz}:

A 2D rotation by θ in the plane:

A 3D rotation by θ in the plane:

A 4D rotation by θ in the plane:

A 3D rotation by θ in the plane parametrized by s{1,-1,1}+t{1,1,1}:

This rotates the vector {1,1,1}:

Generate the transform for a symbolic vector, assuming that all quantities are real:

Simplify the result further by assuming that {x,y,z} is a unit vector:

Transformation applied to a 2D shape:

Transformation applied to a 3D shape:

Applications (5)

Basic (2)

Parametrize a great circle passing through the points u and v on a sphere:

The great circle passing through {1,-1,1}/√3 and {1,1,1}/√3 :

This plots the great circle:

This shows the great circle and points on the unit sphere:

Using GeometricTransformation:

Rotating a character:

Image Transformations (3)

Rotate an image about its {0,0} origin using RotationTransform:

Rotate about the image center:

Specify a different center of rotation in the standard image coordinate system:

Rotate a 3D image around the axis:

Rotate a 3D image around the axis:

Properties & Relations (9)

The rotation transformation is an isometric transform, i.e. preserves distances:

The linear part of a rotation transform is given by RotationMatrix:

The matrix for the linear part is OrthogonalMatrixQ for real rotations:

The inverse of RotationTransform[θ,{u,v}] is RotationTransform[-θ,{u,v}]:

The inverse of RotationTransform[θ,{u,v}] is RotationTransform[θ,{v,u}]:

If u or v is not real, the relationship is more complex:

The inverse of RotationTransform[θ] is given by RotationTransform[-θ]:

The inverse of RotationTransform[θ,w] is given by RotationTransform[-θ,w]:

The inverse of RotationTransform[θ,w] is also given by RotationTransform[θ,-w]:

If w is not real, the relationship is more complex:

The composition of rotations is a rotation:

For graphics transformation, use Rotate:

Possible Issues (1)

The order in which rotations are applied is important:

Compare the results of the two possible orders; the result is not zero:

Neat Examples (1)

Rotate a 3D object about a point p:

Rotate around the axis, in the plane:

Rotate around the axis, in the plane:

Rotate around the axis, in the plane:

Top