RollPitchYawMatrix

RollPitchYawMatrix[{α,β,γ}]

gives the 3D rotation matrix formed by rotating by α around the initial axis, then by β around the initial axis, and then by γ around the initial axis.

RollPitchYawMatrix[{α,β,γ},{a,b,c}]

gives the 3D rotation matrix formed by rotating by α around the fixed a axis, then by β around the fixed b axis, and then by γ around the fixed c axis.

Details and Options

  • RollPitchYawMatrix is also known as bank-elevation-heading matrix or Cardan matrix. The angles {α,β,γ} are often referred to as Cardan angles, Tait–Bryan angles, nautical angles, bank-elevation-heading, or roll-pitch-yaw.
  • RollPitchYawMatrix is typically used to specify a rotation as a sequence of basic rotations around coordinate axes where each rotation is referring to the initial or extrinsic coordinate frame.
  • RollPitchYawMatrix[{α,β,γ}] is equivalent to RollPitchYawMatrix[{α,β,γ},{3,2,1}].
  • RollPitchYawMatrix[{α,β,γ},{a,b,c}] is equivalent to 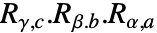where Rα,a=RotationMatrix[α,UnitVector[3,a]] etc.
  • The default z-y-x rotation RollPitchYawMatrix[{α,β,γ},{3,2,1}]:
  • The rotation axes a, b, and c can be any integer 1, 2, or 3, but there are only twelve combinations that are general enough to be able to specify any 3D rotation.
  • Rotations with the first and last axis repeated:
  • {3,2,3}z-y-z rotation
    {3,1,3}z-x-z rotation
    {2,3,2}y-z-y rotation
    {2,1,2}y-x-y rotation
    {1,3,1}x-z-x rotation
    {1,2,1}x-y-x rotation
  • Rotations with all three axes different:
  • {1,2,3}x-y-z rotation
    {1,3,2}x-z-y rotation
    {2,1,3}y-x-z rotation
    {2,3,1}y-z-x rotation
    {3,1,2}z-x-y rotation
    {3,2,1}z-y-x rotation (default)
  • Rotations with subsequent axes repeated still produce a rotation matrix, but cannot be inverted uniquely using RollPitchYawAngles.
  • RollPitchYawMatrix supports the option TargetStructure, which specifies the structure of the returned matrix. Possible settings for TargetStructure include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Orthogonal"represent the matrix as an orthogonal matrix
    "Unitary"represent the matrix as a unitary matrix
  • RollPitchYawMatrix[…,TargetStructureAutomatic] is equivalent to RollPitchYawMatrix[…,TargetStructure"Dense"].

Examples

open allclose all

Basic Examples  (2)

The standard roll-pitch-yaw matrix:

Rotate an axes-aligned unit cube:

Scope  (5)

Give the standard z-y-x roll-pitch-yaw rotation matrix with , , and :

Rotate the vector :

Visualize the rotated vector (red):

Give an x-y-z roll-pitch-yaw rotation matrix by specifying the second argument:

Rotate and visualize the vector {1,0,0}:

Rotate primitives in 3D graphics using GeometricTransformation:

Rotate a region using TransformedRegion:

Rotate a 3D image using ImageTransformation:

Options  (1)

TargetStructure  (1)

Return the roll-pitch-yaw rotation matrix as a dense matrix:

Return the roll-pitch-yaw rotation matrix as an orthogonal matrix:

Return the roll-pitch-yaw rotation matrix as a unitary matrix:

Applications  (6)

Illustrations  (1)

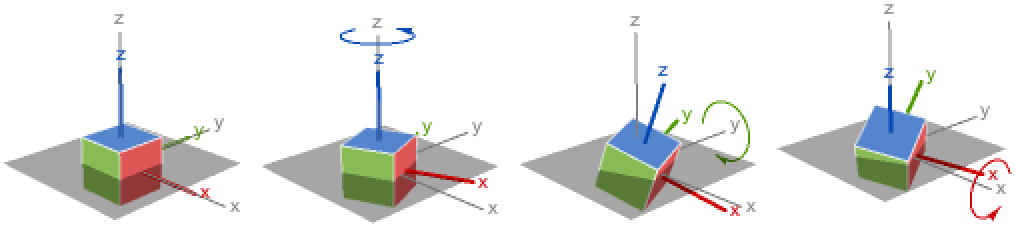
Build a function that illustrates Euler rotations, showing the axis that is being rotated around:

Here are all six of the a-b-c axes rotations. First is the standard z-y-x roll-pitch-yaw rotation:

The x-y-z roll-pitch-yaw rotation:

The x-z-y roll-pitch-yaw rotation:

The y-x-z roll-pitch-yaw rotation:

The y-z-x roll-pitch-yaw rotation:

The z-x-y roll-pitch-yaw rotation:

Then there are the six a-b-a axes rotations. First is the x-y-x roll-pitch-yaw rotation:

The x-z-x roll-pitch-yaw rotation:

The y-x-y roll-pitch-yaw rotation:

The y-z-y roll-pitch-yaw rotation:

The z-x-z roll-pitch-yaw rotation:

The z-y-z roll-pitch-yaw rotation:

Gimbal  (5)

A gimbal is a system of pivoted rings that allows an object to orient itself in an arbitrary direction. These are used in various navigations and imaging applications:

The orientation of the object within a gimbal can be modeled using RollPitchYawMatrix with the angles of the rings' rotations, from the outermost to the innermost rings. Note that an a-b-a axis system is used:

A gimbal with a-b-c axis rotations models a gimbal system with an initial state where all rings' axes are perpendicular to each other:

This uses the x-y-z roll-pitch-yaw rotation:

A rotation system may enter gimbal lock, a situation where a certain angle value reduces the system's degrees of freedom. The normal, non-locked case produces the following:

The vector {1,1,0} can be rotated to an arbitrary point on a surface:

In the locked case, only the difference can affect the rotation:

Now the vector {1,1,0} can only be rotated to a point on a curve:

When axes , gimbal lock will occur when . Here is an example x-y-x rotation:

The non-locked m1 and locked m2 cases:

Unlocked m1 and locked m2 cases for z-y-z rotation:

And when axes are all different , gimbal lock will occur when . Here, when doing an x-y-z rotation:

The locked m1 and unlocked m2 cases:

Locked m1 and unlocked m2 cases for y-x-z rotation:

Properties & Relations  (11)

RollPitchYawMatrix corresponds to three rotations:

With general ordering of rotation axes:

Use RollPitchYawAngles to return angles that produce the same rotation matrix:

The angles need not be the same:

However, both sets of angles produce the same rotation matrix:

RollPitchYawMatrix rotates wrt the global axes (fixed frame) in each step:

EulerMatrix rotates wrt the local axes (moving frame) in each step:

If two subsequent rotation axes are identical, i.e. or , the system has two degrees of freedom, such as here when performing an x-y-y rotation:

If all rotation axes are identical, i.e. , the system has only one degree of freedom, such as here when performing an x-x-x rotation:

RollPitchYawMatrix[{α,β,γ},{a,b,c}] is the same as EulerMatrix[{γ,β,α},{c,b,a}]:

RollPitchYawMatrix parametrizes any rotation in terms of three axis-oriented rotations:

For rotations around a general axis, use RotationMatrix:

RollPitchYawMatrix only applies in :

For general dimension, use RotationMatrix:

RollPitchYawMatrix is an orthogonal matrix with determinant 1:

The inverse of a RollPitchYawMatrix is its transpose:

The inverse of RollPitchYawMatrix[{α,β,γ},{a,b,c}] is RollPitchYawMatrix[{-γ,-β,-α},{c,b,a}]:

Possible Issues  (1)

RollPitchYawMatrix allows equal consecutive axes, and this generates a rotation matrix:

However, RollPitchYawAngles requires consecutive axes to be distinct:

This is because with consecutive axes equal, some rotation matrices cannot be represented:

Neat Examples  (2)

Use GeometricTransformation to visualize the rotation of a sphere by a range of angles:

A collection of randomly rotated tetrahedra:

Wolfram Research (2015), RollPitchYawMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html (updated 2024).

Text

Wolfram Research (2015), RollPitchYawMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html (updated 2024).

CMS

Wolfram Language. 2015. "RollPitchYawMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html.

APA

Wolfram Language. (2015). RollPitchYawMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html

BibTeX

@misc{reference.wolfram_2024_rollpitchyawmatrix, author="Wolfram Research", title="{RollPitchYawMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rollpitchyawmatrix, organization={Wolfram Research}, title={RollPitchYawMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html}, note=[Accessed: 21-December-2024 ]}