is an option that specifies the method to be used for resampling images or arrays.


Resampling
is an option that specifies the method to be used for resampling images or arrays.
Details



- In all of the interpolations, the window is normalized so that its values sum to 1.
- With the setting Resampling->Automatic, the method of resampling is selected automatically.
- Specific settings for Resampling are typically used to achieve different tradeoffs with respect to prefiltering of data, order of interpolation, and complexity of computation.
- Nearest neighbor resamplings are fast, and except for "Nearest" do not introduce any new values:
-
"Nearest" nearest neighbor, use average for tie "NearestLeft" nearest neighbor, use left for tie "NearestRight" nearest neighbor, use right for tie - Spline interpolations are relatively fast, based on polynomial interpolation of order
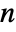 with
with 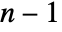 continuous derivatives:
continuous derivatives: -
"Constant" piecewise constant interpolation "Linear" piecewise linear interpolation "Quadratic" spline interpolation of order 2 "Cubic" spline interpolation of order 3 "Quartic" spline interpolation of order 4 "Quintic" spline interpolation of order 5 {"Spline",n} spline interpolation of order up to 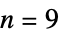
- Gaussian and B-splines of higher orders are practically isotropic resamplings. They are fast approximations that blur the data rather than interpolations:
-
"Gaussian" Gaussian weighted resampling using 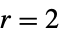 and
and 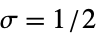
{"Gaussian",r,σ} Gaussian with a specific radius 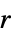 and sigma
and sigma 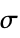
{"BSpline",n} B-spline approximation of order up to 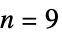
- Classic polynomial interpolations up to order
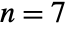 :
: -
"Dodgson" Dodgson polynomial interpolation {"Keys",a} Keys polynomial interpolation (default 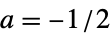 )
)"CatmullRom" Catmull–Rom (Meijering) cubic polynomial interpolation "German" German polynomial interpolation {"Hermite", 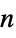 }
}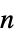
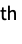 -order Hermite interpolation
-order Hermite interpolation{"Schaum",n} 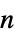
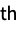 -order Schaum (Lagrange) polynomial interpolation
-order Schaum (Lagrange) polynomial interpolation{"Meijering",n} odd 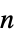
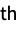 -order Meijering polynomial interpolation
-order Meijering polynomial interpolation - Optimal sampling of maximal order and minimal support (o-MOMS) gives the best resampling for a given order, and may give only continuous or even discontinuous filter kernel:
-
{"OMOMS",n} o-MOMS of order up to 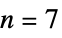
- Windowed sinc interpolations give ideal resamplings regularized by windows of the form
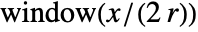 or
or 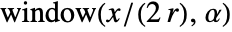 . The following possible window specifications can be given:
. The following possible window specifications can be given: -
{"Bartlett",r} Bartlett (default 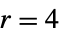 )
){"Blackman",r} Blackman (default 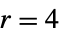 )
){"Connes",r,α} Connes (default 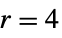 ,
, 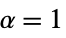 )
){"Cosine",r,α} cosine (default 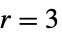 ,
, 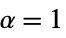 )
){"Hamming",r} Hamming (default 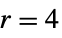 )
){"Hann",r,α} Hann (default 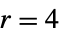 ,
, 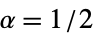 )
){"Kaiser",r,α} Kaiser (default 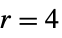 ,
, 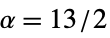 )
){"Lanczos",r} Lanczos (default 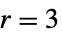 )
){"Parzen",r} Parzen (default 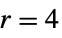 )
){"Welch",r,α} Welch (default 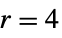 ,
, 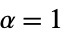 )
)
Tech Notes
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0)
Text
Wolfram Research (2010), Resampling, Wolfram Language function, https://reference.wolfram.com/language/ref/Resampling.html (updated 2014).
CMS
Wolfram Language. 2010. "Resampling." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Resampling.html.
APA
Wolfram Language. (2010). Resampling. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Resampling.html
BibTeX
@misc{reference.wolfram_2025_resampling, author="Wolfram Research", title="{Resampling}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Resampling.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_resampling, organization={Wolfram Research}, title={Resampling}, year={2014}, url={https://reference.wolfram.com/language/ref/Resampling.html}, note=[Accessed: 25-January-2026]}