TuringMachine

TuringMachine[rule,init,t]

generates a list representing the evolution of the Turing machine with the specified rule from initial condition init for t steps.

TuringMachine[rule,init]

gives the result of evolving init for one step.

TuringMachine[rule]

is an operator form of TuringMachine that corresponds to one step of evolution.

Details

  • For a 1D Turing machine, each step in the evolution generated by TuringMachine is given in the form {{s,x,dx},{a1,a2,…}}, where the head is in state s, the cells on the tape have values ai, the head is at position x relative to the ai, and has moved dx relative to its starting position.
  • If dx is omitted in the initial condition for a Turing machine, it is taken to be 0.
  • For a d-dimensional Turing machine, the tape is specified as a d-dimensional array, and the position x and relative position dx are length-d lists.
  • The rule for a Turing machine can be given as a list of replacements of the form {si,ai}->{spi,api,offi}, with elements as follows:
  • sistate of the head
    aivalue of cell under the head
    spinew state of the head
    apinew value of cell under the head
    offioffset by which the head moves
  • The states and cell values can be integers, patterns, or any other expressions. Individual cell values cannot be lists.
  • In one dimension, each offset offi is a single integer; in higher dimensions a list of integers.
  • When the states and cell values are taken to be integers in the range 1 to 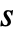s and 0 to 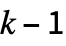k-1 respectively, the following alternative forms can be given for rule:
  • n2‐state, 2‐color machine with number n
    {n,s}s‐state, 2‐color machine with number n
    {n,s,k}s‐state, k‐color machine with number n
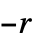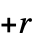    {n,s,k,r}allow offi in the range -r to +r (excluding 0)
    {n,s,k,{r1,r2,…,rd}}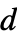d‐dimensional machine with 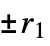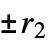+/-r_(1), +/-r_(2), … offsets
    {n,s,k,{{off1},{off2},…}}machine allowing the specified explicit offsets
    {rule,s,k}machine with explicit rule given
    rulemachine with explicit rule given (and s, k inferred)
  • The number of possible Turing machine rules is as follows:
  • 2-state, 2-color machines4096
    s-state, k-color machines(2 s k)^(s k)
    s-state, k-color, range-r machines(2 r s k)^(s k)
    2D s-state, k-color machines(8 s k)^(s k)
  • If the machine has no rule for the configuration it is in, its configuration will not be changed.
  • If a rule has multiple specifications for a given configuration, TuringMachine will use the first one listed.
  • The form {rule,s,k} can be used to specify multiway, non-deterministic and other Turing machines in which there is not necessarily exactly one case in the rule for a given configuration.
  • Typical forms for the initial conditions init are as follows:
  • {s,{{},0}}head in state s, on a 1D tape filled with 0s
    {s,{{a1,a2,…},0}}bounded region of values ai on an infinite tape
    {{s,x},{{a1,a2,…},0}}bounded region with the head initially at position x
    {{s,…},{{a1,…},{b1,…}}}repetitive background of value bi
    {{s,…},{a1,a2,…}}finite tape, assumed cyclic
  • TuringMachine[rule,init,t] generates an evolution list of length t+1.
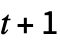  • TuringMachine[rule][init] is equivalent to TuringMachine[rule,init].

Examples

open allclose all

Basic Examples  (5)

2-state, 2-color machine 2506 with an initial tape of four 0s, evolving for 3 steps:

2-state, 2-color machine 2506 with an infinite tape of 0s, evolving for 4 steps:

Plot the successive configurations of the tape:

Show the rule icon for a Turing machine:

Plot the evolution, including the state of the head:

Show the rule icon for a Turing machine specified by explicit transitions:

Plot the evolution, including the state of the head:

A Turing machine specified by pattern-based transition rules:

Scope  (17)

One-Dimensional Rules  (6)

2-state, 2-color machine 2506:

Plot the evolution:

Plot the evolution, including the state of the head:

3-state, 2-color machine 2139050:

Generate a rule icon:

2-state, 2-color machine 16220, with range 2:

3-state, 2-color machine 2139050, with jump offsets and 2:

Give explicit transition rules:

Explicitly specify values of the number of states s and the number of colors k for the same transition rules:

Initial Conditions  (9)

Head Specification  (4)

2-state, 2-color machine 2506 with head initially in state 1:

Evolution:

2-state, 2-color machine 2506 with head initially in state 2:

Evolution:

Place the head at position 3 on the initial tape:

Place the head at position 5 on the initial tape:

Tape Specification  (5)

Start with a finite tape of four 0s, assumed cyclic:

The left neighbor of the leftmost cell is the rightmost cell, and vice versa:

Start with an infinite tape of 0s:

Start with a tape of 1 on an infinite background of 0s:

Start with a tape consisting of the block 211 on a background of 0s:

Start with the block 211 on a background of repeated 02 blocks:

Multidimensional Rules  (2)

2D 2-state, 2-color Turing machine 977401:

2D Turing machine specified by explicit transitions:

Applications  (12)

Evolution of Wolfram's simplest universal Turing machine from an infinite tape of 0s:

Alternative form using explicit rules:

Show the evolutions of a sequence of 2-state, 2-color machines:

Trajectory of the machine head from successive initial conditions:

Path traced by the head of a 2D machine:

Averaging tape of a 2D machine over many steps:

Successive states sequences from successive initial conditions:

Sequence of left or right movements for successive initial conditions:

Halting on a one-sided tape:

Computed function on a one-sided tape:

Show only steps on which the head reaches a new cell:

Show only steps on which the head returns to its initial location:

Causal network from random initial tape:

Properties & Relations  (4)

For rules of the form {n,s,k,…}, head states and cell values can be integers in the range 1 to s and 0 to k-1, respectively:

For rules of the form {n,s,k,…}, if the head reaches a cell whose value is not in the range 0 to k-1, the evolution of the machine halts:

Another Turing machine whose evolution halts:

Use an explicit set of rules to define a halting state:

Plot the evolution:

Generate a Turing machine evolution:

"Inject" the state information into a representation of the tape:

Show the position of the head as a red square:

Use RulePlot to generate a complete evolution picture:

Wolfram Research (2007), TuringMachine, Wolfram Language function, https://reference.wolfram.com/language/ref/TuringMachine.html (updated 2021).

Text

Wolfram Research (2007), TuringMachine, Wolfram Language function, https://reference.wolfram.com/language/ref/TuringMachine.html (updated 2021).

CMS

Wolfram Language. 2007. "TuringMachine." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/TuringMachine.html.

APA

Wolfram Language. (2007). TuringMachine. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TuringMachine.html

BibTeX

@misc{reference.wolfram_2024_turingmachine, author="Wolfram Research", title="{TuringMachine}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/TuringMachine.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_turingmachine, organization={Wolfram Research}, title={TuringMachine}, year={2021}, url={https://reference.wolfram.com/language/ref/TuringMachine.html}, note=[Accessed: 17-November-2024 ]}