BooleanFunction[k,n]
represents the k![]() Boolean function in n variables.
Boolean function in n variables.
BooleanFunction[values]
represents the Boolean function corresponding to the specified vector of truth values.
BooleanFunction[{{i11,i12,…}o1,…}]
represents the Boolean function defined by the specified mapping from inputs to outputs.
BooleanFunction[spec,{a1,a2,…}]
gives the Boolean expression in variables ai corresponding to the Boolean function specified by spec.
BooleanFunction[spec,{a1,a2,…},form]
gives the Boolean expression in the form specified by form.


BooleanFunction
BooleanFunction[k,n]
represents the k![]() Boolean function in n variables.
Boolean function in n variables.
BooleanFunction[values]
represents the Boolean function corresponding to the specified vector of truth values.
BooleanFunction[{{i11,i12,…}o1,…}]
represents the Boolean function defined by the specified mapping from inputs to outputs.
BooleanFunction[spec,{a1,a2,…}]
gives the Boolean expression in variables ai corresponding to the Boolean function specified by spec.
BooleanFunction[spec,{a1,a2,…},form]
gives the Boolean expression in the form specified by form.
Details


- BooleanFunction[spec] gives a Boolean function object that works like Function.
- BooleanFunction[fun] converts a Boolean pure function fun to a Boolean function object.
- BooleanFunction[spec][a1,a2,…] gives an implicit representation equivalent to the explicit Boolean expression BooleanFunction[spec,{a1,a2,…}].
- BooleanConvert converts BooleanFunction[spec][vars] to an explicit Boolean expression.
- In BooleanFunction[values] etc., values can be specified either as True and False or as 1 and 0.
- The functions represented by BooleanFunction always return True or False.
- In BooleanFunction[values], the values are specified in binary order starting with 111, ….
- BooleanFunction[k,n] is equivalent to BooleanFunction[IntegerDigits[k,2,2^n]].
- In BooleanFunction[values], each value can be a list, representing a vector-valued Boolean function.
- In BooleanFunction[{{i11,i12,…}->o1,…}] the oi can be lists, representing vector-valued Boolean functions.
- Elements of both inputs and outputs can be specified either as True and False or as 1 and 0.
- Elements of inputs and outputs can also include any number of _, representing "don't cares".
- They can also include up to one __, representing a sequence of "don't cares".
- In BooleanFunction[spec,{a1,a2,…},form], the possible forms are as given for BooleanConvert.
- BooleanFunction[spec,{a1,a2,…}] by default gives an expression in DNF.
- BooleanFunction[k] gives the k
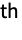 Boolean function in n variables, where n has the smallest value for which
Boolean function in n variables, where n has the smallest value for which 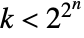 .
. - The numbering of Boolean functions in BooleanFunction[k,…] is consistent with CellularAutomaton.
- BooleanFunction[CellularAutomaton[n]] is equivalent to BooleanFunction[n,3].
- BooleanFunction[CellularAutomaton[{n,2,r}]] is equivalent to BooleanFunction[n,2r+1].
- Operations such as BooleanMinimize, BooleanTable, etc. can operate directly on BooleanFunction objects.
- BooleanFunction objects can be applied to variables just like other Boolean functions such as And, Or, etc.
- In StandardForm and related formats, BooleanFunction objects are printed in elided form, with only their number of variables displayed.
- BooleanVariables gives the number of variables of a BooleanFunction object.
Examples
open all close allBasic Examples (4)
Generate the 30![]() Boolean function of 3 variables:
Boolean function of 3 variables:
Use f like any other Boolean operator:
Generate the formula directly:
Specify a Boolean function based on a table of truth rules:
Use an incompletely specified truth table:
Convert a Boolean expression to a BooleanFunction:
Test that they represent the same function:
Convert Boolean pure functions to BooleanFunction objects:
Scope (14)
Basic Uses (3)
Create a BooleanFunction with two arguments by indexing:
Compute its value for particular arguments:
The function remains unevaluated for symbolic arguments:
BooleanFunction can be used just like any other Boolean operator:
Any Boolean expression can be converted to a BooleanFunction expression:
Including combinations of BooleanFunction expressions:
A BooleanFunction expression that is equivalent to True or False automatically simplifies:
BooleanFunction is a canonical representation, and equivalence can be tested using SameQ:
Working with Truth Tables (7)
Create a truth table in standard order:
Create an equivalent BooleanFunction expression:
Show that they are equivalent:
Alternatively, show that the resulting truth tables are the same:
Create a complete list of truth rules:
Create the corresponding BooleanFunction expression:
The ordering of truth rules for complete lists has no effect:
Use _ to indicate "don't cares" in a truth table:
Create a BooleanFunction:
The resulting truth table matches the original specification:
Use _ and __ to indicate "don't cares" in truth rules:
Create a BooleanFunction:
The original rules completely specify the function and the resulting truth tables are identical:
Use lists of lists to indicate a vector-valued truth table:
Create a BooleanFunction:
The resulting output matches the original specification:
Use vector-valued truth rules:
Create a BooleanFunction:
The resulting truth rules match the original specification:
Truth tables can also be given using 0 in place of False and 1 in place of True:
Working with Other Representations (4)
Convert any Boolean expression to a BooleanFunction expression:
Show that they are equivalent:
Convert expressions involving any Boolean operators:
Show that they are equivalent:
Convert a BooleanFunction expression to other standard forms:
A number of different standard forms:
Specify BooleanFunction using CellularAutomaton:
Applications (4)
Enumerating Boolean Functions (2)
Creating New Primitives (1)
Create new Boolean primitives corresponding to ≤, ≥, <, and >:
Implies is equivalent to x<=y:
Define a relation for Boolean functions f≼g iff ![]() f[u]≤g[u]:
f[u]≤g[u]:
Here you have x≼x∨y as reflected in the truth tables:
For all Boolean functions f and g, f∧g≼f≼f∨g:
Properties & Relations (7)
BooleanFunction displays in an elided form indicating the number of arguments:
The InputForm gives an encoding that can be used to reconstruct the object:
Use the encoding to construct a BooleanFunction:
The result is identical to the original:
The order of values for BooleanFunction is the same as BooleanTable:
The corresponding BooleanFunction has an identical truth table:
The ordering is consistent with Tuples:
Indexing of BooleanFunction is consistent with IntegerDigits:
Convert from a BooleanFunction to its index:
Convert from any Boolean expression to its index:
Show that it is equivalent with the indexed BooleanFunction expression:
The indexing of Boolean functions agrees with the indexing of cellular automata:
More generally, for CellularAutomaton[{k,2,r}] with integer ![]() and
and ![]() , the relation reads:
, the relation reads:
CellularAutomaton satisfying the preceding properties can be used to specify BooleanFunction:
BooleanMinterms can also represent any BooleanFunction:
The mapping from minterms to index:
The mapping from index to minterms:
Use BooleanConvert to convert to BooleanFunction from other forms:
Also use BooleanConvert to convert from BooleanFunction to other forms:
Show that they are all equivalent:
Use BooleanTable to convert BooleanFunction to truth tables:
Related Guides
History
Text
Wolfram Research (2008), BooleanFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/BooleanFunction.html.
CMS
Wolfram Language. 2008. "BooleanFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BooleanFunction.html.
APA
Wolfram Language. (2008). BooleanFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BooleanFunction.html
BibTeX
@misc{reference.wolfram_2025_booleanfunction, author="Wolfram Research", title="{BooleanFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BooleanFunction.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_booleanfunction, organization={Wolfram Research}, title={BooleanFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/BooleanFunction.html}, note=[Accessed: 04-March-2026]}