AngleVector[θ]
gives the list representing the 2D unit vector at angle θ relative to the ![]() axis.
axis.
AngleVector[{r,θ}]
gives the list representing the 2D vector of length r at angle θ.
AngleVector[{x,y},θ]
gives the result of starting from the point {x,y}, then going a unit distance at angle θ.
AngleVector[{x,y},{r,θ}]
gives the result of starting from the point {x,y}, then going distance r at angle θ.


AngleVector
AngleVector[θ]
gives the list representing the 2D unit vector at angle θ relative to the ![]() axis.
axis.
AngleVector[{r,θ}]
gives the list representing the 2D vector of length r at angle θ.
AngleVector[{x,y},θ]
gives the result of starting from the point {x,y}, then going a unit distance at angle θ.
AngleVector[{x,y},{r,θ}]
gives the result of starting from the point {x,y}, then going distance r at angle θ.
Details
- Unless explicitly given as a Quantity object, the angle θ is assumed to be in radians, counterclockwise starting from the
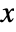 axis. (Multiply by Degree to convert from degrees.)
axis. (Multiply by Degree to convert from degrees.) - AngleVector[{r,θ}] gives a vector that starts at {0,0}.
- The arguments of AngleVector can be symbolic. They can also be Quantity objects.
Examples
open all close allBasic Examples (4)
Angles are assumed to be in radians:
Use a Quantity angle instead:
Scope (5)
Properties & Relations (4)
For short displacements around a geo location, AngleVector approximates GeoDestination:
Move 10 kilometers with initial bearing of 40°:
Re-express that position in terms of a Cartesian frame centered at London:
The horizontal displacement vector in meters is approximately the following:
Folding of AngleVector can be used to move from a point along a sequence of {r,θ} displacements:
The same result can be achieved with AnglePath, using angles relative to the previous segment:
ListPolarPlot can be interpreted as a combination of AngleVector and ListPlot:
ListPolarPlot takes pairs {θi,ri}, but AngleVector takes pairs {r,θ}, so Reverse is needed:
Related Guides
History
Text
Wolfram Research (2015), AngleVector, Wolfram Language function, https://reference.wolfram.com/language/ref/AngleVector.html.
CMS
Wolfram Language. 2015. "AngleVector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AngleVector.html.
APA
Wolfram Language. (2015). AngleVector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AngleVector.html
BibTeX
@misc{reference.wolfram_2025_anglevector, author="Wolfram Research", title="{AngleVector}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AngleVector.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_anglevector, organization={Wolfram Research}, title={AngleVector}, year={2015}, url={https://reference.wolfram.com/language/ref/AngleVector.html}, note=[Accessed: 05-March-2026]}