WOLFRAM

Wolfram Language & System Documentation Center

CirclePoints[n]

gives the positions of n points equally spaced around the unit circle.

CirclePoints[r,n]

gives the positions of n points equally spaced around a circle of radius r.

CirclePoints[{r,θ1},n]

starts at angle θ1 with respect to the axis.

CirclePoints[{x,y},rspec,n]

centers the circle at {x,y}.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Properties & Relations  
Interactive Examples  
Neat Examples  
See Also
Related Guides
History
Cite this Page

CirclePoints

CirclePoints[n]

gives the positions of n points equally spaced around the unit circle.

CirclePoints[r,n]

gives the positions of n points equally spaced around a circle of radius r.

CirclePoints[{r,θ1},n]

starts at angle θ1 with respect to the axis.

CirclePoints[{x,y},rspec,n]

centers the circle at {x,y}.

Details

  • For positive integer n, CirclePoints[n] generates a list of vertices for a regular n-sided polygon, oriented so its base is horizontal.
  • In CirclePoints[n], n does not have to be an exact integer. The angles between successive vectors are always .
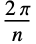  • Unless explicitly given as a Quantity object, the angle θ1 is assumed to be in radians, counterclockwise starting from the 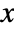axis. (Multiply by Degree to convert from degrees.)
  • If the angle θ1 is not given, it is assumed to be π/n-π/2, so that for integer n the vectors correspond to a regular polygon with its base horizontal.
  • All arguments of CirclePoints except n can be symbolic. They can also be Quantity objects.

Examples

open all close all

Basic Examples  (3)

Corners of an equilateral triangle:

Draw a pentagon:

Draw unit vectors to the corners of a regular heptagon:

Scope  (6)

Corners of a centered square with horizontal and vertical sides:

Corners of a square of size :

Four unitary vectors aligned with the axes:

Displace them to a different point:

The four corners of an arbitrary square, at any point and any size or orientation:

Use a Quantity radius:

Specify the initial angle as a Quantity object:

Draw polygons, with their lowest side oriented horizontally by default:

Draw them all together, with opacity:

Properties & Relations  (2)

CirclePoints returns pairs that can be reinterpreted as real and imaginary parts of the roots of unity:

CirclePoints is equivalent to a collection of AngleVector calls:

Interactive Examples  (1)

Construct polygons of different sizes and number of sides:

Neat Examples  (2)

Combine Fold and CirclePoints:

Combine CirclePoints with BezierCurve:

Wolfram Research (2015), CirclePoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CirclePoints.html.

Text

Wolfram Research (2015), CirclePoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CirclePoints.html.

CMS

Wolfram Language. 2015. "CirclePoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CirclePoints.html.

APA

Wolfram Language. (2015). CirclePoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CirclePoints.html

BibTeX

@misc{reference.wolfram_2025_circlepoints, author="Wolfram Research", title="{CirclePoints}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/CirclePoints.html}", note=[Accessed: 31-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_circlepoints, organization={Wolfram Research}, title={CirclePoints}, year={2015}, url={https://reference.wolfram.com/language/ref/CirclePoints.html}, note=[Accessed: 31-October-2025]}