WOLFRAM

Wolfram Language & System Documentation Center

ImageCooccurrence[image,n]

gives the n×n co-occurrence matrix for image.

ImageCooccurrence[image,n,ker]

computes a co-occurrence matrix for arbitrary spatial relationships specified by a kernel ker.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Options  
Masking  
Applications  
Properties & Relations  
See Also
Related Guides
History
Cite this Page

ImageCooccurrence

ImageCooccurrence[image,n]

gives the n×n co-occurrence matrix for image.

ImageCooccurrence[image,n,ker]

computes a co-occurrence matrix for arbitrary spatial relationships specified by a kernel ker.

Details and Options

  • ImageCooccurrence[image,n] returns an n×n matrix m whose elements mij represent the probability of all occurrences of a pixel with intensity i to the left or bottom of a pixel with intensity j, assuming all pixels to lie in one of n successive bins.
  • With ImageCooccurrence[image,n,ker], the co-occurrence matrix can be computed for arbitrary spatial relationships specified by a matrix ker.
  • The default two-dimensional kernel used by ImageCooccurrence is .
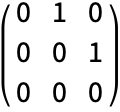  • ImageCooccurrence[{image1,image2},…] computes the co-occurrence matrix across two images. The images must have the same dimensions.
  • ImageCooccurrence supports a Masking option. The default setting is Masking->All, constructing the co-occurrence matrix based on all of the image pixels.

Examples

open all close all

Basic Examples  (2)

A co-occurrence matrix:

3D profile of a co-occurrence matrix:

Scope  (4)

Graylevel co-occurrence matrix, computed for a color image:

Joint histogram of two color channels of the same image:

Specify a horizontally symmetric kernel:

Specify a diagonal kernel that matches the pattern of the image:

Options  (1)

Masking  (1)

Use a binary mask to specify the region of interest:

Applications  (2)

Define a function that computes the Haralick texture contrast measure:

Contrast of a checkerboard image and a flat image:

Haralick texture correlation measure for grayscale images:

Compute the horizontal correlation:

Vertical correlation:

Properties & Relations  (4)

Co-occurrence matrix of a random image:

The total of all elements of the co-occurrence matrix is 1:

Co-occurrence matrix of a checkerboard image:

Co-occurrence matrix of a striped image using a horizontal kernel:

Wolfram Research (2010), ImageCooccurrence, Wolfram Language function, https://reference.wolfram.com/language/ref/ImageCooccurrence.html.

Text

Wolfram Research (2010), ImageCooccurrence, Wolfram Language function, https://reference.wolfram.com/language/ref/ImageCooccurrence.html.

CMS

Wolfram Language. 2010. "ImageCooccurrence." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ImageCooccurrence.html.

APA

Wolfram Language. (2010). ImageCooccurrence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImageCooccurrence.html

BibTeX

@misc{reference.wolfram_2025_imagecooccurrence, author="Wolfram Research", title="{ImageCooccurrence}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ImageCooccurrence.html}", note=[Accessed: 11-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_imagecooccurrence, organization={Wolfram Research}, title={ImageCooccurrence}, year={2010}, url={https://reference.wolfram.com/language/ref/ImageCooccurrence.html}, note=[Accessed: 11-August-2025]}