WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

KochCurve

KochCurve[n]

第 n ステップのコッホ(Koch)曲線を表す線分を与える．

KochCurve[n,{θ1,θ2,…}]

連続する相対角度 θiで単位長の一連のステップを取る．

KochCurve[n,{{r1,θ1},{r2,θ2},…}]

長さが riに比例する，連続するステップを取る．

詳細とオプション

  • KochCurveはコッホ雪片としても知られている．
  • KochCurve[n]は，セルの真ん中3分の1を削除し，それを三角形で置換することを繰り返すことで単位区間から生成される． »
  • KochCurve[n]はKochCurve[n,{0,60 °,-120 °,60 °}]に等しい．
  • KochCurveは，座標が占めるであろうと考えられる範囲の指定に使うことができるDataRangeオプションを取る．

例題

すべて開くすべて閉じる

例  (2)基本的な使用例

2Dコッホ曲線：

コッホメッシュの近似の長さ：

式は以下のようになる：

コッホ雪片の最初の4回の繰返し：

スコープ  (7)標準的な使用例のスコープの概要

曲線指定  (3)

2Dコッホ曲線：

コッホ曲線の第 n ステップの近似：

相対角度の長さを指定する：

曲線のスタイル  (4)

太さの異なるコッホ曲線：

太さはスケールされたサイズである：

印刷用ポイント数による太さ：

破線曲線：

色付きの曲線：

オプション  (1)各オプションの一般的な値と機能

DataRange  (1)

DataRangeを使うと生成するメッシュ座標の範囲を指定することができる：

別の範囲を指定する：

アプリケーション  (4)この関数で解くことのできる問題の例

KochCurveは，セルを三等分し，その中央部分を三角形で置換することの繰り返しで生成される：

Cesàroフラクタルを生成する：

二次タイプ1曲線：

二次タイプ2曲線：

特性と関係  (3)この関数の特性および他の関数との関係

KochCurveは直線からなる：

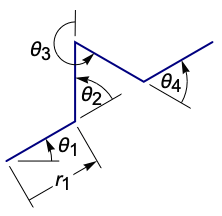
AnglePathを使ってコッホ曲線の最初の反復を生成することができる：

DataRange -> range はRescalingTransform[{...},range]を使うことに等しい：

RescalingTransformを使う：

おもしろい例題  (1)驚くような使用例や興味深い使用例

コッホ雪片のアニメーション：

Wolfram Research (2017), KochCurve, Wolfram言語関数， https://reference.wolfram.com/language/ref/KochCurve.html.

テキスト

Wolfram Research (2017), KochCurve, Wolfram言語関数， https://reference.wolfram.com/language/ref/KochCurve.html.

CMS

Wolfram Language. 2017. "KochCurve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KochCurve.html.

APA

Wolfram Language. (2017). KochCurve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KochCurve.html

BibTeX

@misc{reference.wolfram_2025_kochcurve, author="Wolfram Research", title="{KochCurve}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/KochCurve.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_kochcurve, organization={Wolfram Research}, title={KochCurve}, year={2017}, url={https://reference.wolfram.com/language/ref/KochCurve.html}, note=[Accessed: 04-April-2025 ]}