KroneckerSymbol

KroneckerSymbol[n,m]

gives the Kronecker symbol .

Details

  • KroneckerSymbol is also known as the Jacobi symbol or Legendre symbol.
  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • KroneckerSymbol[n,1] gives 1.
  • KroneckerSymbol[n,-1] gives 1 whenever n is non-negative and 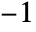otherwise.
  • For a number 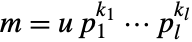with 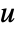a unit and 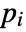primes, TemplateBox[{n, m}, KroneckerSymbol] returns TemplateBox[{n, u}, KroneckerSymbol] TemplateBox[{n, {p, _, 1}}, KroneckerSymbol] ...TemplateBox[{n, {p, _, l}}, KroneckerSymbol].

Examples

open allclose all

Basic Examples  (2)

Compute Kronecker symbols:

Plot the KroneckerSymbol sequence with respect to the second argument:

Scope  (9)

Numerical Evaluation  (3)

KroneckerSymbol works over integers:

Compute for large arguments:

KroneckerSymbol threads elementwise over lists:

Symbolic Manipulation  (6)

TraditionalForm formatting:

Reduce expressions:

Solve equations:

Use KroneckerSymbol in a sum:

Recurrence equation:

Generating function:

Applications  (11)

Basic Applications  (2)

Table of values of the Kronecker symbol with n, m up to 10:

Plot the nontrivial values of the Kronecker symbol:

Number Theory  (9)

For congruent integers m and n modulo p, KroneckerSymbol[m,p]==KroneckerSymbol[n,p]:

Find Euler–Jacobi pseudoprimes to base : [more info]

The law of quadratic reciprocity for distinct primes n and m :

Construct eigenvectors of the discrete Fourier transform:

Evaluate Gauss sums in closed form:

The congruence equation has a solution if KroneckerSymbol[a,p] == 1:

KroneckerSymbol[n,k] is a real DirichletCharacter modulo k for odd integers k:

A real primitive character χ modulo k can be written in terms of KroneckerSymbol[χ[-1]k,n]:

Nonprimitive real characters can be written in terms of KroneckerSymbol at integers coprime to k:

KroneckerSymbol is the generalization of the Jacobi symbol for all integers:

Properties & Relations  (5)

KroneckerSymbol gives for non-coprime integers:

KroneckerSymbol is a completely multiplicative function for each argument:

The law of quadratic reciprocity for distinct primes n and m :

Use KroneckerSymbol to compute real DirichletCharacter modulo k for odd integers k:

Check that the following relation holds for any odd integer:

Neat Examples  (4)

The array plot of KroneckerSymbol:

Plot the arguments of the Fourier transform of KroneckerSymbol:

Successive differences of KroneckerSymbol modulo 2:

Plot the Ulam spiral of KroneckerSymbol:

Wolfram Research (2007), KroneckerSymbol, Wolfram Language function, https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

Text

Wolfram Research (2007), KroneckerSymbol, Wolfram Language function, https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

CMS

Wolfram Language. 2007. "KroneckerSymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

APA

Wolfram Language. (2007). KroneckerSymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KroneckerSymbol.html

BibTeX

@misc{reference.wolfram_2024_kroneckersymbol, author="Wolfram Research", title="{KroneckerSymbol}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/KroneckerSymbol.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kroneckersymbol, organization={Wolfram Research}, title={KroneckerSymbol}, year={2007}, url={https://reference.wolfram.com/language/ref/KroneckerSymbol.html}, note=[Accessed: 21-December-2024 ]}