DirichletCharacter[k,j,n]
gives the Dirichlet character ![]() with modulus k and index j.
with modulus k and index j.


DirichletCharacter
DirichletCharacter[k,j,n]
gives the Dirichlet character ![]() with modulus k and index j.
with modulus k and index j.
Details
- Integer mathematical function, suitable for both symbolic and numerical manipulation.
- DirichletCharacter[k,j,n] picks a particular ordering for possible Dirichlet characters modulo k.
- There are ϕ
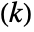 distinct Dirichlet characters for a given modulus k, as labeled by the index j. Different conventions can give different orderings for the possible characters.
distinct Dirichlet characters for a given modulus k, as labeled by the index j. Different conventions can give different orderings for the possible characters. - DirichletCharacter[k,j,n] is periodic in n with period k.
- DirichletCharacter[k,j,n] is zero when n is not coprime to k.
- DirichletCharacter[k,j,n] is a multiplicative function in n.
Examples
open all close allScope (3)
Compute the Dirichlet transform:
DirichletCharacter threads element-wise over lists:
Applications (5)
Compute the number of primitive Dirichlet characters modulo ![]() :
:
Define generalized Bernoulli numbers from DirichletCharacter:
Compute values at negative integers of DirichletL using generalized Bernoulli numbers:
The generalized Bernoulli number at 0 of a principal character is ![]() and zero otherwise:
and zero otherwise:
Dirichlet characters modulo ![]() form a group:
form a group:
Operations on Dirichlet characters:
The product of ![]() and its character modulo
and its character modulo ![]() at values coprime to
at values coprime to ![]() gives Gauss sums:
gives Gauss sums:
For primitive characters modulo ![]() ,
, ![]() are zero at values not coprime to
are zero at values not coprime to ![]() :
:
For primitive characters modulo ![]() , absolute values of Gauss sums are equal to
, absolute values of Gauss sums are equal to ![]() :
:
Find conductors of Dirichlet characters modulo ![]() with
with ![]() an odd prime power:
an odd prime power:
DirichletCharacter[25,11,n] has a conductor 5:
Properties & Relations (11)
DirichletCharacter is periodic:
DirichletCharacter is completely multiplicative:
Values of Dirichlet characters are equal to zero or roots of unity:
DirichletCharacter modulo ![]() is nonzero at values coprime to
is nonzero at values coprime to ![]() :
:
DirichletCharacter modulo ![]() is zero at values not coprime to
is zero at values not coprime to ![]() :
:
The trivial character takes the value ![]() for all integers:
for all integers:
A principal character modulo ![]() has index
has index ![]() and gives
and gives ![]() for values coprime to
for values coprime to ![]() ; otherwise it gives
; otherwise it gives ![]() :
:
Real Dirichlet characters modulo ![]() have index
have index ![]() or
or ![]() :
:
JacobiSymbol[n,k] is a real Dirichlet character modulo k for odd integers k:
A real primitive character χ modulo k can be defined as JacobiSymbol[χ[-1]k,n]:
Nonprimitive real characters can be written in terms of JacobiSymbol at integers coprime to ![]() :
:
DirichletCharacter[k,j,n] gives ![]() at the primitive root n of k, when it exists:
at the primitive root n of k, when it exists:
Use the multiplicative property of DirichletCharacter to get values at integers coprime to ![]() :
:
A character modulo ![]() can be written as a product of characters modulo prime powers of
can be written as a product of characters modulo prime powers of ![]() :
:
First find primitive roots of 32 and 5:
Find exponents of 7 modulo 32 and 5:
Dirichlet characters are labeled in an increasing order of the number of factors:
Decomposition of the Dirichlet character modulo 32 5 with index 8:
Verify the decomposition formula for all integers coprime to 32 5:
Lift a Dirichlet character modulo 3 to a Dirichlet character modulo a power of 3:
See Also
Related Guides
History
Text
Wolfram Research (2008), DirichletCharacter, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletCharacter.html.
CMS
Wolfram Language. 2008. "DirichletCharacter." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DirichletCharacter.html.
APA
Wolfram Language. (2008). DirichletCharacter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletCharacter.html
BibTeX
@misc{reference.wolfram_2025_dirichletcharacter, author="Wolfram Research", title="{DirichletCharacter}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DirichletCharacter.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_dirichletcharacter, organization={Wolfram Research}, title={DirichletCharacter}, year={2008}, url={https://reference.wolfram.com/language/ref/DirichletCharacter.html}, note=[Accessed: 22-January-2026]}