DirichletL

DirichletL[k,j,s]

gives the Dirichlet L-function for the Dirichlet character with modulus k and index j.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For 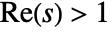, , 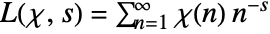where 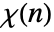is a Dirichlet character.
  • The possible Dirichlet characters 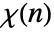modulo k are specified by an index j, and given by DirichletCharacter[k,j,n].
  • DirichletL[k,j,s] can be evaluated to arbitrary numerical precision for integer k and j, and arbitrary complex s.
  • DirichletL automatically threads over lists.
  • DirichletL can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (2)

A plot along the line 1+ ω:

Scope  (5)

Evaluate for complex arguments:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Simple exact values are generated automatically:

DirichletL threads element-wise over lists and matrices:

DirichletL can be used with Interval and CenteredInterval objects:

Applications  (4)

Plot the real part of a DirichletL function on the critical line:

Plot the real part across the critical strip:

Find a zero of a DirichletL function:

Plot real and imaginary parts in the vicinity of nearby zeros:

Neat Examples  (1)

The real part of a Dirichlet L-function:

Wolfram Research (2008), DirichletL, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletL.html (updated 2023).

Text

Wolfram Research (2008), DirichletL, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletL.html (updated 2023).

CMS

Wolfram Language. 2008. "DirichletL." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/DirichletL.html.

APA

Wolfram Language. (2008). DirichletL. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletL.html

BibTeX

@misc{reference.wolfram_2025_dirichletl, author="Wolfram Research", title="{DirichletL}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/DirichletL.html}", note=[Accessed: 13-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_dirichletl, organization={Wolfram Research}, title={DirichletL}, year={2023}, url={https://reference.wolfram.com/language/ref/DirichletL.html}, note=[Accessed: 13-May-2025 ]}