JacobiSymbol

JacobiSymbol[n,m]

gives the Jacobi symbol .

Details

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • For prime m, the Jacobi symbol reduces to the Legendre symbol. The Legendre symbol is equal to 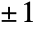depending on whether n is a quadratic residue modulo m.
  • JacobiSymbol automatically threads over lists.

Examples

open allclose all

Basic Examples  (2)

Compute Jacobi symbols:

Plot the sequence wrt the last argument:

Scope  (3)

Evaluate for large arguments:

Second argument may be even:

TraditionalForm formatting:

Generalizations & Extensions  (2)

JacobiSymbol threads element-wise over lists and arrays:

JacobiSymbol works for negative first arguments:

Applications  (5)

Find Euler–Jacobi pseudoprimes:

The Gauss reciprocity law:

Construct eigenvectors of the discrete Fourier transform:

Evaluate Gauss sums in closed form:

Plot the nontrivial values of the Jacobi symbol:

Properties & Relations  (1)

Reduce equations containing JacobiSymbol:

Neat Examples  (1)

Successive differences of JacobiSymbol modulo 2:

Wolfram Research (1988), JacobiSymbol, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiSymbol.html.

Text

Wolfram Research (1988), JacobiSymbol, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiSymbol.html.

CMS

Wolfram Language. 1988. "JacobiSymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiSymbol.html.

APA

Wolfram Language. (1988). JacobiSymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiSymbol.html

BibTeX

@misc{reference.wolfram_2024_jacobisymbol, author="Wolfram Research", title="{JacobiSymbol}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/JacobiSymbol.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jacobisymbol, organization={Wolfram Research}, title={JacobiSymbol}, year={1988}, url={https://reference.wolfram.com/language/ref/JacobiSymbol.html}, note=[Accessed: 21-November-2024 ]}