WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

KroneckerSymbol[n,m]

クロネッカー(Kronecker)の記号を与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
記号演算  
アプリケーション  
基本的なアプリケーション  
整数論  
特性と関係  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

KroneckerSymbol

KroneckerSymbol[n,m]

クロネッカー(Kronecker)の記号を与える．

詳細

  • KroneckerSymbolはヤコビ(Jacobi)の記号またはルジャンドル(Legendre)の記号としても知られている．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • KroneckerSymbol[n,1]は1を与える．
  • KroneckerSymbol[n,-1]は n が非負のときは常に1を与える．それ以外の場合は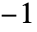を与える．
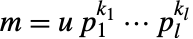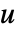  • TemplateBox[{n, m}, KroneckerSymbol]は数 （ は単数で 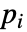は素数）についてTemplateBox[{n, u}, KroneckerSymbol] TemplateBox[{n, {p, _, 1}}, KroneckerSymbol] ...TemplateBox[{n, {p, _, l}}, KroneckerSymbol]を返す．

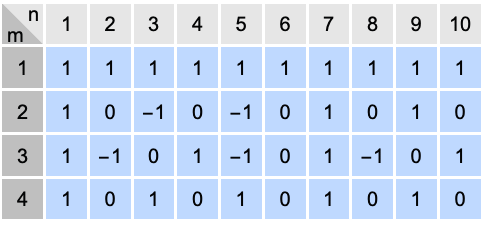
例題

すべて開く すべて閉じる

例  (2)

クロネッカーの記号を計算する：

Wolfram Language code: KroneckerSymbol[17, 6]
Wolfram Language code: Table[KroneckerSymbol[n, m], {n, 5}, {m, 5}]

KroneckerSymbol数列を第2引数についてプロットする：

Wolfram Language code: DiscretePlot[KroneckerSymbol[7, m], {m, 50}]

スコープ  (9)

数値評価  (3)

KroneckerSymbolは整数に使うことができる：

Wolfram Language code: KroneckerSymbol[10, 13]

大きい引数について計算する：

Wolfram Language code: KroneckerSymbol[10 ^ 11 + 1, Prime[2000]]

KroneckerSymbolは要素単位でリストに縫い込まれる：

Wolfram Language code: KroneckerSymbol[{2, 3, 5, 7, 11}, 6]

記号演算  (6)

TraditionalFormによる表示：

Wolfram Language code: KroneckerSymbol[n, m]//TraditionalForm

式を簡約する：

Wolfram Language code: Reduce[KroneckerSymbol[p, 3] == 2 KroneckerSymbol[p + 1, 3] - 1 && -5 < p < 5, {p}, Integers]

方程式を解く：

Wolfram Language code: Solve[KroneckerSymbol[n, 5] == 1 && 0 < n < 5, n, Integers]

KroneckerSymbolを総和で使う：

Wolfram Language code: Sum[KroneckerSymbol[a, 16], a]

式を簡約する：

Wolfram Language code: DifferenceRootReduce[KroneckerSymbol[n, 7], n]

母関数：

Wolfram Language code: GeneratingFunction[KroneckerSymbol[n, 7], n, x]

アプリケーション  (11)

基本的なアプリケーション  (2)

n と m が10までのクロネッカー記号の値の表：

Wolfram Language code: Grid[Table[If[n m == 0 , If[n + m == 0, " ", Style[n + m, Red, Italic, Bold]], KroneckerSymbol[n, m]], {n, 0, 10}, {m, 0, 10}], ...]

クロネッカー記号の自明な値をプロットする：

Wolfram Language code: ArrayPlot[Table[KroneckerSymbol[n, m], {n, 0, 40}, {m, 1, 2n, 2}], ColorRules -> {1 -> Red, -1 -> Blue}]

整数論  (9)

p を法とする合同な整数 m と n についてKroneckerSymbol[m,p]==KroneckerSymbol[n,p]である：

Wolfram Language code: Mod[2, 7] == Mod[23, 7]
Wolfram Language code: KroneckerSymbol[2, 7] == KroneckerSymbol[23, 7]

基数がのオイラー・ヤコビ擬似素数を求める [詳細]：

Wolfram Language code: pseudoPrimeQ[n_Integer] := GCD[n, 2] === 1 && CompositeQ[n] && KroneckerSymbol[2, n] == Mod[2 ^ ((n - 1) / 2), n];
Wolfram Language code: Select[Range[10000], pseudoPrimeQ]

異なる素数 n と m の平方剰余の相互法則：

Wolfram Language code: {n, m} = {11, 13};
Wolfram Language code: PrimeQ[{n, m}]
Wolfram Language code: KroneckerSymbol[n, m ]KroneckerSymbol[m, n] == (-1) ^ ((n - 1)(m - 1) / 4)

離散フーリエ(Fourier)変換の固有ベクトルを構築する：

Wolfram Language code: With[{p = 13}, Table[KroneckerSymbol[k, p], {k, 0, p - 1}]]//N
Wolfram Language code: Fourier[%]

ガウス和を閉じた形で評価する：

Wolfram Language code: GaussSum[h_, p_] := KroneckerSymbol[h, p] I^((p - 1/2))^2 Sqrt[p] - 1;
Wolfram Language code: GaussSum[4, 11]

合同方程式 はKroneckerSymbol[a,p] == 1であれば解を持つ：

Wolfram Language code: KroneckerSymbol[2, 7]
Wolfram Language code: PowerMod[2, 1 / 2, 7]

KroneckerSymbol[n,k]は奇整数 k について k を法とした実数のDirichletCharacterである：

Wolfram Language code: Table[KroneckerSymbol[n, 5], {n, 0, 4}]
Wolfram Language code: Table[DirichletCharacter[5, 3, n], {n, 0, 4}]

k を法とした実数の原始指標 χ はKroneckerSymbol[χ[-1]k,n]によって書くことができる：

Wolfram Language code: Table[DirichletCharacter[7, 4, n], {n, 0, 6}]
Wolfram Language code: Table[KroneckerSymbol[DirichletCharacter[7, 4, -1] * 7, n], {n, 0, 6}]

非原始的な実数指標は k と互いに素な整数においてKroneckerSymbolによって書くことができる：

Wolfram Language code: DirichletCharacter[12, 3, {1, 5, 7, 11}]
Wolfram Language code: KroneckerSymbol[-4, {1, 5, 7, 11}]

KroneckerSymbolはすべての整数についてヤコビ記号を一般化したものである：

Wolfram Language code: jacobi[n_, m_] := KroneckerSymbol[n, m] /; (OddQ[m] && Positive[m]);
Wolfram Language code: Table[jacobi[2, m], {m, 1, 9}]

特性と関係  (5)

KroneckerSymbolは互いに素ではない整数についてはを与える：

Wolfram Language code: CoprimeQ[9, 12]
Wolfram Language code: KroneckerSymbol[9, 12]

KroneckerSymbolは，各引数について完全に乗法的な関数である：

Wolfram Language code: KroneckerSymbol[3 4, 7] == KroneckerSymbol[3, 7]KroneckerSymbol[4, 7]
Wolfram Language code: KroneckerSymbol[3, 9 7] == KroneckerSymbol[3, 9]KroneckerSymbol[3, 7]

異なる整数 n と m についての平方剰余の相互法則：

Wolfram Language code: {n, m} = {11, 13};
Wolfram Language code: PrimeQ[{n, m}]
Wolfram Language code: KroneckerSymbol[n, m] KroneckerSymbol[m, n] == (-1) ^ ((n - 1)(m - 1) / 4)

KroneckerSymbolを使って奇整数 k について k を法とする実数のDirichletCharacterを計算する：

Wolfram Language code: Table[KroneckerSymbol[n, 5], {n, 0, 4}]
Wolfram Language code: Table[DirichletCharacter[5, 3, n], {n, 0, 4}]

次の関係が任意の奇整数について成り立つことを確かめる：

Wolfram Language code: n = 39; KroneckerSymbol[-1, n] == (-1)^(n - 1/2)

おもしろい例題  (4)

KroneckerSymbolの配列プロット：

Wolfram Language code: ArrayPlot[Table[KroneckerSymbol[n, m], {n, -50, 50}, {m, -50, 50}], ColorRules -> {-1 -> Black, 0 -> White, 1 -> Blue}]

KroneckerSymbolのフーリエ変換の引数をプロットする：

Wolfram Language code: ArrayPlot[Arg[Fourier[Table[KroneckerSymbol[m, n], {m, 100}, {n, 100}]]], ColorFunction -> Hue]

2を法としたKroneckerSymbolの逐次差分：

Wolfram Language code: ArrayPlot[Mod[NestList[Differences, KroneckerSymbol[Range[100], 77], 100], 2]]

KroneckerSymbolのウラム(Ulam)螺線をプロットする：

Wolfram Language code: ulam[n_] := Partition[Permute[Range[n ^ 2], Accumulate[Take[Flatten[{{n ^ 2 + 1} / 2, Table [(-1) ^ j i, {j, n}, {i, {-1, n}}, {j}]}], n ^ 2]]], n];
Wolfram Language code: ArrayPlot[KroneckerSymbol[70, ulam[125]], ColorFunction -> "BlueGreenYellow"]
Wolfram Research (2007), KroneckerSymbol, Wolfram言語関数， https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

テキスト

Wolfram Research (2007), KroneckerSymbol, Wolfram言語関数， https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

CMS

Wolfram Language. 2007. "KroneckerSymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KroneckerSymbol.html.

APA

Wolfram Language. (2007). KroneckerSymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KroneckerSymbol.html

BibTeX

@misc{reference.wolfram_2026_kroneckersymbol, author="Wolfram Research", title="{KroneckerSymbol}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/KroneckerSymbol.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_kroneckersymbol, organization={Wolfram Research}, title={KroneckerSymbol}, year={2007}, url={https://reference.wolfram.com/language/ref/KroneckerSymbol.html}, note=[Accessed: 02-November-2026]}