LineGraph
Details and Options

- Each vertex in LineGraph[g] corresponds to an edge in g.
- For an undirected graph g, two vertices in LineGraph[g] are adjacent if their corresponding edges share a common vertex.
- For a directed graph g, two vertices in LineGraph[g] are adjacent if their corresponding edges are connected, i.e. the target of one edge is the source of the other edge.
- The vertices in LineGraph[g] are taken to be successive integers starting at 1.
- LineGraph works with undirected graphs, directed graphs, and multigraphs.
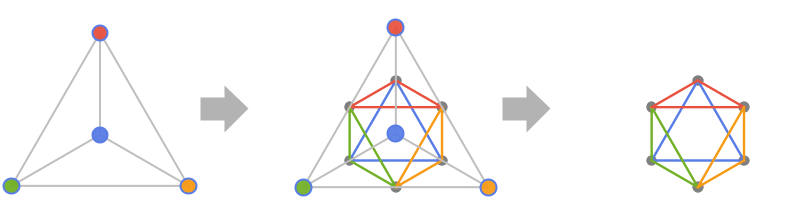
Background & Context
- LineGraph returns the line graph
 of
of  , which is the graph whose vertices are the edges of
, which is the graph whose vertices are the edges of  and whose vertex adjacencies correspond to the edge adjacencies of
and whose vertex adjacencies correspond to the edge adjacencies of 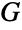 . More formally, given a graph
. More formally, given a graph 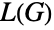 with edges e1,…,em,
with edges e1,…,em, 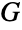 has vertices e1,…,em. For undirected
has vertices e1,…,em. For undirected  ,
, 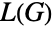 is an edge in
is an edge in 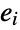 if
if 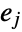 and
and 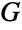 are incident to the same vertex in
are incident to the same vertex in 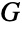 , while for directed
, while for directed  ,
, 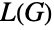 is an edge in
is an edge in 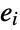 if the head of
if the head of 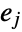 is the tail of
is the tail of  in
in 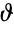 . A line graph is also known as an adjoint graph, conjugate graph, covering graph, derivative graph, derived graph, edge graph, edge-to-vertex dual graph, interchange graph, representative graph, or
. A line graph is also known as an adjoint graph, conjugate graph, covering graph, derivative graph, derived graph, edge graph, edge-to-vertex dual graph, interchange graph, representative graph, or 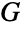 -obrazom graph.
-obrazom graph. - Line graphs are used to translate graph theoretical results about vertices to results about edges. For example, independent edge sets in
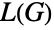 are independent vertex sets in
are independent vertex sets in 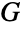 , the edge chromatic number of
, the edge chromatic number of 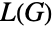 is equal to the chromatic number of
is equal to the chromatic number of 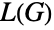 , etc.
, etc. - Line graphs are connected by a number of mathematical relations to their original graphs. The simplest of these is that the number of vertices of
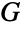 equals the number of edges of
equals the number of edges of 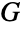 . In addition, if
. In addition, if 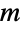 is a simple graph having
is a simple graph having 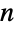 edges and
edges and 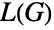 vertices with vertex degrees d1,…,dn, then the number of edges in
vertices with vertex degrees d1,…,dn, then the number of edges in 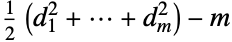 is
is 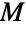 . Another relation that allows explicit construction of line graphs is that for
. Another relation that allows explicit construction of line graphs is that for 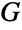 the incidence matrix of a simple graph
the incidence matrix of a simple graph 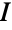 and
and 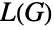 an m×m identity matrix, the adjacency matrix for
an m×m identity matrix, the adjacency matrix for 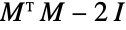 is given by
is given by 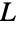 .
. - Determining whether a graph is a line graph can be done in linear time. A graph
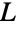 is the line graph of a simple graph or multigraph if and only if there exists a family of cliques such that each vertex in
is the line graph of a simple graph or multigraph if and only if there exists a family of cliques such that each vertex in 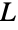 is contained in exactly two of them, and each edge in
is contained in exactly two of them, and each edge in 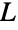 is induced by one of them.
is induced by one of them. 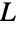 is the line graph of a simple graph if this family of cliques can be formed so that no two vertices of
is the line graph of a simple graph if this family of cliques can be formed so that no two vertices of 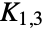 lie in the same two cliques.
lie in the same two cliques. - There is a set of nine forbidden graphs, each having at most six vertices, such that a simple graph is a line graph of some simple graph if and only if it contains no graph in this set as an induced subgraph. This set of forbidden graphs is given by GraphData["Beineke"] and includes the complete bipartite graph
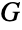 , so line graphs are claw-free. Only six of these forbidden graphs are needed to characterize which simple graphs having maximum degree at least 5 are line graphs (see GraphData["Metelsky"]).
, so line graphs are claw-free. Only six of these forbidden graphs are needed to characterize which simple graphs having maximum degree at least 5 are line graphs (see GraphData["Metelsky"]). - Many important results in graph theory characterize the properties of line graphs. For example, Vizing's theorem implies that if
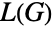 is a triangle-free simple graph, then the chromatic number of
is a triangle-free simple graph, then the chromatic number of 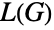 is either equal to or one more than the size of a maximum clique in
is either equal to or one more than the size of a maximum clique in 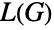 , while König's line coloring theorem implies that the line graph
, while König's line coloring theorem implies that the line graph 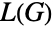 of a bipartite graph is perfect (i.e. the chromatic number of every induced subgraph of
of a bipartite graph is perfect (i.e. the chromatic number of every induced subgraph of 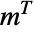 equals the size of the largest clique of that subgraph).
equals the size of the largest clique of that subgraph).
Examples
open all close allScope (5)
Properties & Relations (11)
The number of edges in a graph is equal to the number of vertices in its line graph:
The line graph of a connected graph is connected:
The adjacency matrix of a line graph can be computed by ![]()
![]() :
:
A maximum independent set in a line graph of g corresponds to the maximum matching of g:
A cycle graph is isomorphic to its line graph:
The line graph of a claw ![]() is a triangle:
is a triangle:
The line graph of a path ![]() is isomorphic to
is isomorphic to ![]() :
:
The line graph of a bipartite graph is perfect:
The line graph of a Hamiltonian graph is Hamiltonian:
Neat Examples (1)
Related Guides
Text
Wolfram Research (2010), LineGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/LineGraph.html (updated 2015).
CMS
Wolfram Language. 2010. "LineGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/LineGraph.html.
APA
Wolfram Language. (2010). LineGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LineGraph.html
BibTeX
@misc{reference.wolfram_2025_linegraph, author="Wolfram Research", title="{LineGraph}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/LineGraph.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_linegraph, organization={Wolfram Research}, title={LineGraph}, year={2015}, url={https://reference.wolfram.com/language/ref/LineGraph.html}, note=[Accessed: 05-January-2026]}

