MatrixGamePayoff
MatrixGamePayoff[mgame,{s1,…,sn}]
给出矩阵博弈 mgame 中每个玩家的预期收益,其中策略配置为 {s1,…,sn}.
MatrixGamePayoff[mgame,{s1,…,sn},"prop"]
给出每个玩家的收益属性 "prop".
MatrixGamePayoff[mgame,"player1"s1,…,"playern"sn]
使用关联给出矩阵博弈 mgame 中每个命名玩家的预期收益,其中策略配置为 {s1,…,sn}.
更多信息

- MatrixGamePayoff 亦称为预期收益或预期效用.
- MatrixGamePayoff 通常用于计算每个玩家的预期收益,其中每个玩家的策略已知.
- 策略配置
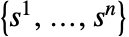 是
是 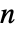 个玩家的策略列表. 玩家
个玩家的策略列表. 玩家 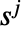 的策略
的策略 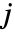 是采取不同动作的概率向量
是采取不同动作的概率向量 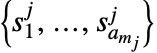 .
. - 玩家
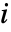 的预期收益为
的预期收益为  或
或 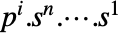 ,其中:
,其中: -
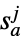
玩家 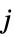 采取动作
采取动作 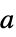 的概率
的概率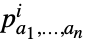
当玩家 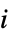 采取动作
采取动作 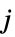 时玩家
时玩家 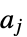 的收益
的收益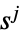
玩家 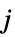 的策略
的策略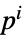
玩家 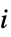 的收益数组
的收益数组 - 收益属性 "prop" 包括:
-
"Expectation" 每个玩家的平均收益 "MarginalDistributions" 每个玩家的收益分布 "MultivariateDistribution" 所有玩家收益的多元分布 "Simulation" 对一轮博弈随机生成的收益列表 {"Simulation", n} 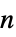 轮博弈的收益列表
轮博弈的收益列表"Variance" 每个玩家的收益方差
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (5)
应用 (7)
社会学博弈 (2)
经济学博弈 (2)
军事博弈 (1)
交通博弈 (1)
令人惊讶的是,当在道路网络中添加一条或多条道路时,可能会导致整体交通状况变差,这被称为布雷斯悖论. 已知从 a 到 b 有两条不同的路径,一条经过 c,一条经过 d. 道路 ac 和 db 需要 20 n 分钟,其中 n 是道路上的驾驶员数量;cb 和 ad 需要 45 分钟,与驾驶员数量无关. 将道路网络表示为图:
按照上面的交通博弈,一般道路网络的建模和求解可以实现自动化. 这里的 start 和 end 是始顶点和终顶点,每个道路段的容量使用边权重进行编码:
在两条先前存在的路线之间切换的新可能性导致了类似囚徒困境的情形,其中唯一稳定的解导致与受限网络(65 分钟)相比更长的通勤时间(82 分钟):
文本
Wolfram Research (2025),MatrixGamePayoff,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
CMS
Wolfram 语言. 2025. "MatrixGamePayoff." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
APA
Wolfram 语言. (2025). MatrixGamePayoff. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixGamePayoff.html 年