MeanNeighborDegree

MeanNeighborDegree[g]

グラフ g の頂点の平均近傍次数のリストを与える．

MeanNeighborDegree[g,"In"]

平均近傍入次数のリストを与える．

MeanNeighborDegree[g,"Out"]

平均近傍出次数のリストを与える．

MeanNeighborDegree[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細

  • 平均近傍次数は平均値近傍次数としても知られている．
  • 頂点 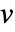の平均近傍次数は 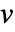の近傍の頂点次数の平均である．
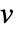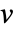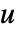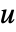  • 重み付きグラフの場合，頂点 の平均近傍次数は， のすべての近傍 について， と 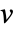の間の辺重みを 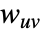として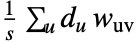で与えられる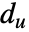．は頂点 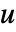の次数であり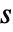， は重み 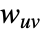の合計である．
  • MeanNeighborDegreeは，無向グラフ，有向グラフ，重み付きグラフ．多重グラフ，混合グラフに使うことができる．

例題

すべて開くすべて閉じる

例  (2)

平均近傍次数を計算する：

ハイライトする：

頂点をランク付けする．最高ランクの頂点は高次数頂点に隣接している：

スコープ  (8)

MeanNeighborDegreeは無向グラフに使うことができる：

有向グラフに使う：

重み付きグラフに使う：

多重グラフに：

混合グラフに：

規則を使ってグラフを指定する：

平均近傍入次数および出次数を計算する：

MeanNeighborDegreeは大きいグラフに使うことができる：

アプリケーション  (4)

自律システムのレベルでインターネット接続の平均回数を求める：

ネットワークに高次数のハブがあると平均近傍次数が高くなる：

arXiv e-Printアーカイブの「高エネルギー物理現象」セクションからの引用ネットワーク．1論文あたりの引用の平均数を計算する：

引用として引用する論文の平均数：

参考文献の平均数を計算する：

参考文献として引用された論文の平均数：

Zachary空手クラブのネットワーク中のソーシャルハブをハイライトする：

ニュージーランド，ダウトフルサウンド沖に生息するイルカの間に見られる絆のソーシャルネットワーク：

絆が1つしかないイルカが9つ以上の絆を持つイルカの近傍にいる確率を計算する：

派生モデルで確率を求める：

特性と関係  (4)

孤立頂点の平均近傍次数は0である：

有向辺は無向辺として扱われる：

VertexDegreeを使って平均近傍次数を計算する：

MeanDegreeConnectivityは次数で集められた頂点の平均を与える：

3平均次数連結度を求める：

次数3の頂点を求める：

平均近傍次数の平均：

Wolfram Research (2012), MeanNeighborDegree, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeanNeighborDegree.html （2015年に更新）.

テキスト

Wolfram Research (2012), MeanNeighborDegree, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeanNeighborDegree.html （2015年に更新）.

CMS

Wolfram Language. 2012. "MeanNeighborDegree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/MeanNeighborDegree.html.

APA

Wolfram Language. (2012). MeanNeighborDegree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanNeighborDegree.html

BibTeX

@misc{reference.wolfram_2024_meanneighbordegree, author="Wolfram Research", title="{MeanNeighborDegree}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/MeanNeighborDegree.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_meanneighbordegree, organization={Wolfram Research}, title={MeanNeighborDegree}, year={2015}, url={https://reference.wolfram.com/language/ref/MeanNeighborDegree.html}, note=[Accessed: 03-December-2024 ]}