gives a list of mean neighbor degrees of vertices for the graph g.
MeanNeighborDegree[g,"In"]
gives a list of mean neighbor in-degrees.
MeanNeighborDegree[g,"Out"]
gives a list of mean neighbor out-degrees.
MeanNeighborDegree[{vw,…},…]
uses rules vw to specify the graph g.


MeanNeighborDegree
gives a list of mean neighbor degrees of vertices for the graph g.
MeanNeighborDegree[g,"In"]
gives a list of mean neighbor in-degrees.
MeanNeighborDegree[g,"Out"]
gives a list of mean neighbor out-degrees.
MeanNeighborDegree[{vw,…},…]
uses rules vw to specify the graph g.
Details
- The mean neighbor degree is also known as the average neighbor degree.
- The mean neighbor degree of the vertex
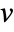 is the mean of vertex degrees of neighbors of
is the mean of vertex degrees of neighbors of 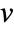 .
. - For weighted graphs, the mean neighbor degree of the vertex
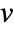 is given by
is given by 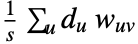 over all neighbors
over all neighbors 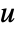 of
of 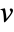 with edge weight
with edge weight 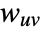 between
between 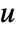 and
and 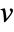 .
. 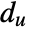 is the degree of the vertex
is the degree of the vertex 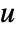 and
and 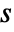 is the total of weights
is the total of weights 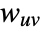 .
. - MeanNeighborDegree works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.
Examples
open all close allBasic Examples (2)
Scope (8)
MeanNeighborDegree works with undirected graphs:
Use rules to specify the graph:
Compute the mean neighbor in- and out-degree:
MeanNeighborDegree works with large graphs:
Applications (4)
Find the average number of connections for the internet at the level of autonomous systems:
The presence of high-degree hubs in the network increases the mean neighbor degree:
A citation network from the High Energy Physics Phenomenology section of the arXiv e-Print archive. Compute the average number of citations per article:
The mean number of citing articles for citations:
Compute the average number of references:
The mean number of cited articles for references:
Highlight social hubs in the Zachary karate club network:
A social network of frequent association ties between dolphins living off Doubtful Sound, NZ:
Compute the probability that a dolphin with just one tie has a neighbor with nine ties or more:
Properties & Relations (4)
Isolated vertices have mean neighbor degree 0:
Directed edges are treated as undirected:
Use VertexDegree to compute the mean neighbor degree:
MeanDegreeConnectivity gives the means over vertices gathered by degree:
See Also
MeanDegreeConnectivity VertexDegree VertexInDegree VertexOutDegree
Function Repository: HypergraphNeighborhoodVolumes
Related Guides
Text
Wolfram Research (2012), MeanNeighborDegree, Wolfram Language function, https://reference.wolfram.com/language/ref/MeanNeighborDegree.html (updated 2015).
CMS
Wolfram Language. 2012. "MeanNeighborDegree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/MeanNeighborDegree.html.
APA
Wolfram Language. (2012). MeanNeighborDegree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanNeighborDegree.html
BibTeX
@misc{reference.wolfram_2025_meanneighbordegree, author="Wolfram Research", title="{MeanNeighborDegree}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/MeanNeighborDegree.html}", note=[Accessed: 01-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_meanneighbordegree, organization={Wolfram Research}, title={MeanNeighborDegree}, year={2015}, url={https://reference.wolfram.com/language/ref/MeanNeighborDegree.html}, note=[Accessed: 01-January-2026]}