Multinomial

Multinomial[n1,n2,…]

多項係数を与える．

詳細

  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • 多項係数Multinomial[n1,n2,…]は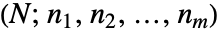，を表し，それぞれの大きさを 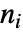(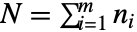)とする 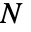個の個別のオブジェクトを 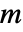組に分割する方法の数を与える．
  • Multinomialは，自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (5)

数値的に評価する：

1, 2, 1の多項係数がx y^2 zの係数として現れている：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける級数展開：

スコープ  (27)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率よく評価する：

Aroundを使って平均的な場合の統計区間を計算する：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のMultinomial関数を計算することもできる：

特定の値  (4)

固定点におけるMultinomialの値：

記号的な n についてのMultinomial：

ゼロにおける値：

Multinomial[n,1,1]=15となるような n の値を求める：

可視化  (2)

Multinomialをパラメータの関数としてプロットする：

6 TemplateBox[{{z, +, 6}, z}, Binomial]の実部をプロットする：

6 TemplateBox[{{z, +, 6}, z}, Binomial]の虚部をプロットする：

関数の特性  (11)

最後のパラメータ の関数としてのの実領域：

複素領域：

の値域を近似する：

は鏡特性を持つ：

は x の解析関数である：

は非減少でも非増加でもない：

は単射ではない：

は全射である：

は非負でも非正でもない：

は特異点も不連続点も持たない：

は凸でも凹でもない：

TraditionalFormによる表示：

微分  (2)

n3についての一次導関数：

n3についての高次導関数：

n1=n2=3のとき，n3についての高次導関数をプロットする：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

一般化と拡張  (1)

Multinomialはリストに対して要素単位で適用される：

アプリケーション  (4)

多項定理を例証する：

要素を3つのボックスに入れる方法の数の等値面をプロットする：

多項確率分布：

超楕円体 の体積はである：

直接積分したものと比べてみる：

特性と関係  (4)

引数が2つの場合，Multinomialは二項係数を与える：

FullSimplifyを使って多項係数を含む式を簡約する：

FunctionExpandを使って関数にGamma関数に展開する：

MultinomialはOrderlessである：

考えられる問題  (3)

大きい引数は明示的に計算をするのには大きすぎる結果を与えることがある：

機械数の入力で高精度の結果が得られることがある：

多変数関数として，Multinomialは負の整数についてはすべての変数において連続的ではない：

おもしろい例題  (3)

2を法とする三項式：

3を法とする：

複素平面上でネストした多項式：

Multinomialを複素引数についてプロットする：

Wolfram Research (1988), Multinomial, Wolfram言語関数， https://reference.wolfram.com/language/ref/Multinomial.html.

テキスト

Wolfram Research (1988), Multinomial, Wolfram言語関数， https://reference.wolfram.com/language/ref/Multinomial.html.

CMS

Wolfram Language. 1988. "Multinomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Multinomial.html.

APA

Wolfram Language. (1988). Multinomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Multinomial.html

BibTeX

@misc{reference.wolfram_2024_multinomial, author="Wolfram Research", title="{Multinomial}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Multinomial.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multinomial, organization={Wolfram Research}, title={Multinomial}, year={1988}, url={https://reference.wolfram.com/language/ref/Multinomial.html}, note=[Accessed: 21-December-2024 ]}