NegativeReals

NegativeReals

represents the domain of strictly negative real numbers.

Details

  • x∈NegativeReals evaluates immediately if x is a numeric quantity.
  • Simplify[expr∈NegativeReals,assum] can be used to try to determine whether an expression corresponds to a negative real number under the given assumptions.
  • (x1|x2|…)∈NegativeReals and {x1,x2,…}∈NegativeReals test whether all xi are negative real numbers.
  • NegativeReals is output in StandardForm and TraditionalForm as 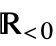. This typeset form can be input using nreals.

Examples

open allclose all

Basic Examples  (3)

is a negative real number:

If is a real number, is a negative real number:

Find negative real solutions of an equation:

Scope  (4)

Test if a numeric quantity is negative:

Make domain membership assumptions:

Specify the default domain over which a function should work:

Test whether several numbers are negative reals:

If any number is explicitly not a negative number, the result is False:

Applications  (1)

Testing membership in the negative reals is a fast way to verify negativity of a large list:

Properties & Relations  (4)

Membership in NegativeReals is equivalent to membership in Reals along with negativity:

NegativeReals contains NegativeRationals and NegativeIntegers:

NegativeReals is contained in Complexes:

NegativeReals is disjoint from NonNegativeReals and PositiveReals:

Wolfram Research (2019), NegativeReals, Wolfram Language function, https://reference.wolfram.com/language/ref/NegativeReals.html.

Text

Wolfram Research (2019), NegativeReals, Wolfram Language function, https://reference.wolfram.com/language/ref/NegativeReals.html.

CMS

Wolfram Language. 2019. "NegativeReals." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NegativeReals.html.

APA

Wolfram Language. (2019). NegativeReals. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativeReals.html

BibTeX

@misc{reference.wolfram_2024_negativereals, author="Wolfram Research", title="{NegativeReals}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/NegativeReals.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_negativereals, organization={Wolfram Research}, title={NegativeReals}, year={2019}, url={https://reference.wolfram.com/language/ref/NegativeReals.html}, note=[Accessed: 21-November-2024 ]}