NeighborhoodGraph

NeighborhoodGraph[g,v]

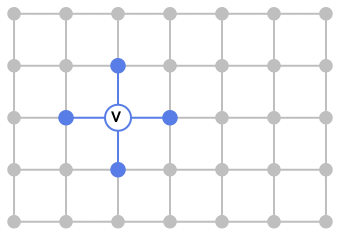
gives the graph neighborhood of a vertex v in the graph g.

NeighborhoodGraph[g,{a1,a2,…}]

gives the graph neighborhood of the ai that can be vertices, edges, or subgraphs of g.

NeighborhoodGraph[g,patt]

gives the graph neighborhood of the vertices and edges that match the pattern patt.

NeighborhoodGraph[g,…,d]

gives the neighborhood up to distance d.

NeighborhoodGraph[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • The neighborhood graph for a vertex v is given by vertices adjacent to v and the edges connecting them.
  • The neighborhood graph for an edge e is the neighborhood graph for the vertices of e.
  • The neighborhood graph for a subgraph h is the neighborhood graph for the vertices in h.
  • The neighborhood graph at distance d is the neighborhood graph for the vertices of the neighborhood graph at distance d-1.
  • The default value for d is 1.
  • NeighborhoodGraph works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (2)

Give the neighborhood from vertex 1 in a graph:

From a set of vertices:

Give the neighborhood up to distance k from the vertices:

Scope  (8)

NeighborhoodGraph works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

NeighborhoodGraph works with vertices:

Edges:

Use rules to specify the graph:

Use patterns to specify a set of vertices:

NeighborhoodGraph works with large graphs:

Applications  (2)

Highlight the neighborhood from the vertices in CompleteGraph:

CycleGraph:

StarGraph:

GridGraph:

CompleteKaryTree:

PathGraph:

RandomGraph:

Manipulate the neighborhood of vertices:

Properties & Relations  (2)

Use Subgraph to find the neighborhood graph of a set of vertices:

Highlight the subgraph:

This is equivalent to:

The neighborhood of a vertex in a complete graph is the graph itself:

Neat Examples  (2)

Pick out random neighborhoods from a grid:

Subtract random neighborhoods from a grid:

Wolfram Research (2010), NeighborhoodGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/NeighborhoodGraph.html (updated 2015).

Text

Wolfram Research (2010), NeighborhoodGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/NeighborhoodGraph.html (updated 2015).

CMS

Wolfram Language. 2010. "NeighborhoodGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/NeighborhoodGraph.html.

APA

Wolfram Language. (2010). NeighborhoodGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NeighborhoodGraph.html

BibTeX

@misc{reference.wolfram_2024_neighborhoodgraph, author="Wolfram Research", title="{NeighborhoodGraph}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/NeighborhoodGraph.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_neighborhoodgraph, organization={Wolfram Research}, title={NeighborhoodGraph}, year={2015}, url={https://reference.wolfram.com/language/ref/NeighborhoodGraph.html}, note=[Accessed: 21-November-2024 ]}