NumberDigit
NumberDigit[x,n]
returns the digit corresponding to 10n in the real-valued number x.
NumberDigit[x,n,b]
returns the digit corresponding to b![]() .
.
Details
- The digit to the immediate left of the decimal point is the
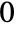
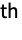 digit.
digit. - In NumberDigit[x,…], x can be any real-valued numeric expression.
- NumberDigit[x,{n1,n2,…}] returns {NumberDigit[x,n1],NumberDigit[x,n2],…}.
- In NumberDigit[x,n,b], the base b must be a real-valued number greater than 1.
- NumberDigit is listable in its first argument.
Examples
open allclose allBasic Examples (2)
Scope (7)
Find the 104 and 106 digits of a number:
Find the 103, 105 and 107 digits in a number:
Find the 102 through 10-2 digits of Pi:
Find the 102 through 10-2 digits of Pi in base 16:
Find the first three digits of the fraction
:Digits of negative numbers are the same as for their positive counterparts:
The base need not be an integer, and you can find the first several digits of Pi to a base strictly between 1 and 2:
These are not the same as the digits to corresponding powers in base 2:
NumberDigit is listable in its first argument:
Applications (2)
Properties & Relations (1)
NumberDigit[x,n,b] returns the digit given as the first element of RealDigits[x,b,1,n]:
Possible Issues (1)
Text
Wolfram Research (2021), NumberDigit, Wolfram Language function, https://reference.wolfram.com/language/ref/NumberDigit.html.
CMS
Wolfram Language. 2021. "NumberDigit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NumberDigit.html.
APA
Wolfram Language. (2021). NumberDigit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NumberDigit.html