NumberDigit

NumberDigit[x,n]

returns the digit corresponding to 10n in the real-valued number x.

NumberDigit[x,n,b]

returns the digit corresponding to b^(n).

Details

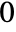
  • The digit to the immediate left of the decimal point is the 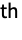^(th) digit.
  • In NumberDigit[x,…], x can be any real-valued numeric expression.
  • NumberDigit[x,{n1,n2,…}] returns {NumberDigit[x,n1],NumberDigit[x,n2],…}.
  • In NumberDigit[x,n,b], the base b must be a real-valued number greater than 1.
  • NumberDigit is listable in its first argument.

Examples

open allclose all

Basic Examples  (2)

Find the digit corresponding to 102 in a number:

Find the digit corresponding to 10-1 in a number:

Scope  (7)

Find the 104 and 106 digits of a number:

Find the 103, 105 and 107 digits in a number:

Find the 102 through 10-2 digits of Pi:

Find the 102 through 10-2 digits of Pi in base 16:

Find the first three digits of the fraction

:

Digits of negative numbers are the same as for their positive counterparts:

The base need not be an integer, and you can find the first several digits of Pi to a base strictly between 1 and 2:

These are not the same as the digits to corresponding powers in base 2:

NumberDigit is listable in its first argument:

Applications  (2)

Show that the fourth digit of random reals between 0 and 1 is equally distributed over the range from 0 through 9:

Take all days of the year 2021:

Histogram of the ^(th) digits of months:

Histogram of the ^(th) digits of days:

Histogram of the ^(st) digits of days:

Properties & Relations  (1)

NumberDigit[x,n,b] returns the digit given as the first element of RealDigits[x,b,1,n]:

Possible Issues  (1)

For an approximate real value, if the requested digit(s) are beyond the input precision, then the result will have indeterminate digits:

Neat Examples  (1)

Take a thousand sums of a hundred reals between 0 and 1:

They are distributed around 50:

Because the deviation is smaller than 10, there is a nonuniform distribution of ^(th) digits:

Wolfram Research (2021), NumberDigit, Wolfram Language function, https://reference.wolfram.com/language/ref/NumberDigit.html.

Text

Wolfram Research (2021), NumberDigit, Wolfram Language function, https://reference.wolfram.com/language/ref/NumberDigit.html.

CMS

Wolfram Language. 2021. "NumberDigit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NumberDigit.html.

APA

Wolfram Language. (2021). NumberDigit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NumberDigit.html

BibTeX

@misc{reference.wolfram_2024_numberdigit, author="Wolfram Research", title="{NumberDigit}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/NumberDigit.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_numberdigit, organization={Wolfram Research}, title={NumberDigit}, year={2021}, url={https://reference.wolfram.com/language/ref/NumberDigit.html}, note=[Accessed: 21-December-2024 ]}