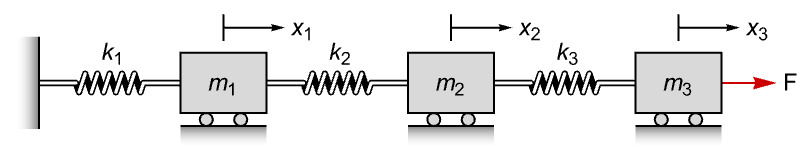
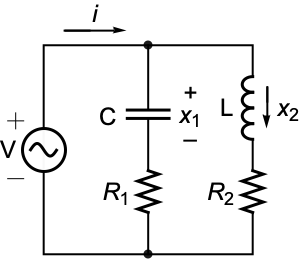
ObservableModelQ

ObservableModelQ[sys]

系 sys が可観測であればTrueを，それ以外の場合はFalseを与える．

ObservableModelQ[{sys,sub}]

部分系 sub が可観測であればTrueを与える．

詳細とオプション

  • 有限時間における 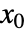からのモデルの軌跡がその近傍からの他の状態の軌跡と識別可能な場合，その状態空間モデルは 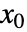において可観測であると言われる．
  • 系 sys は標準およびディスクリプタのStateSpaceModelあるいはAffineStateSpaceModelでよい．
  • 次の部分系 sub を指定することができる．
  • All系全体
    "Fast"速い部分系
    "Slow"遅い部分系
    "Unstable"不安定な部分系
    {λ1,…}固有モード 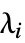lambda_(i)の部分系
  • KroneckerModelDecompositionにあるように，"Fast"と"Slow"の部分系が主にディスクリプタ状態空間モデルに適用される．
  • 固有モード λiについてはJordanModelDecompositionに記述されている．
  • ObservableModelQには以下の設定のMethodオプションが使える．
  • Automatic適切な検定を自動的に選ぶ
    "Distribution"可観測性分布の階数を使う
    "Gramian"可観測性グラミアンの階数または正定性を使う
    "Matrix"可観測性行列の階数を使う
    "PBH"Popov–Belevitch–Hautus階数検定を使う

例題

すべて開くすべて閉じる

例  (2)

可観測系：

非可観測系（第2状態が可観測ではないため）：

スコープ  (6)

近似係数を持つ系の可観測性を検定する：

厳密係数：

記号係数：

多出力系：

離散時間系：

ディスクリプタ系：

可観測性は速いモードと遅い部モード両方が可観測であることと等しい（C可観測性）：

個々の固有モードの可観測性を検定する：

固有モードがあるので，この系は可観測ではない：

これは，第2状態を観測する術がないジョルダン系にも見ることができる：

AffineStateSpaceModelの可観測性を検定する：

操作点 が与えられているなら，における可観測性が検定できる：

この系は生成点において可観測である：

オプション  (6)

Method  (6)

デフォルトで，可観測性行列は厳密系および記号系に用いられる：

ObservabilityMatrixが最大階数であれば，この系は可観測である：

可観測性グラミアンは安定した数値系に用いられる：

ObservabilityGramianが最大階数であれば，この系は可観測である：

可観測性グラミアンについては，このことは，これが正定値であることと等しい：

PBH階数検定は，他のすべての数値系に用いられる：

がすべての について最大階数なので，この系は可観測である：

可観測性共分布は，入力線形系に用いられる：

線形系については，可観測性行列と共分布に基づいた検定は等しい：

線形系の可観測性は，入力線形系の可観測性を暗示する：

入力線形系についての行列検定は，線形化された系について"Matrix"メソッドを用いる：

アプリケーション  (2)

の測定から3つの質量すべての位置と速度を推定することができる：

状態としてのコンデンサー電圧とインダクタ電流，測度としての電流 がある電気回路：

一般に，この系は可観測である：

しかし， 野場合は可観測ではない：

特性と関係  (6)

および を仮定すると，対角系は可観測である：

のとき，最初の状態を観測する方法はない：

のとき，2番目の状態は直接観測することはできないが，最初の状態を通して間接的に観測することができる：

のとき，最初の状態は，直接観測することmp2番目の状態から間接的に観測することもできない：

JordanModelDecompositionで，上記の標準状態空間表現を計算する：

"PBH"検定を使って各モードのか観測性を計算する：

ディスクリプタ系については，KroneckerModelDecompositionは対角系形の一般化である：

遅い部分系の可観測性をその構造から調べる：

もとの系を使ってこれを計算する：

速い部分系の可観測性をの構造から調べる：

もとの系を使ってこれを計算する：

StateSpaceModelのディスクリプタ行列が最大階数であれば，速い部分系は存在しない：

したがって，系の完全な可制御性は遅い部分系から評価できる：

AffineStateSpaceModelについては，入力ベクトルの非線形性が可観測性を助ける：

線形入力ベクトルのある系は可観測ではない：

可観測ではない系は，区別できない初期状態を持つ：

およびの2つの初期状態は，区別できない出力を生成する：

考えられる問題  (1)

漸近的に安定ではない系についてはグラミアンメソッドは信頼できない：

Wolfram Research (2010), ObservableModelQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservableModelQ.html （2014年に更新）.

テキスト

Wolfram Research (2010), ObservableModelQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservableModelQ.html （2014年に更新）.

CMS

Wolfram Language. 2010. "ObservableModelQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ObservableModelQ.html.

APA

Wolfram Language. (2010). ObservableModelQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservableModelQ.html

BibTeX

@misc{reference.wolfram_2024_observablemodelq, author="Wolfram Research", title="{ObservableModelQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ObservableModelQ.html}", note=[Accessed: 07-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_observablemodelq, organization={Wolfram Research}, title={ObservableModelQ}, year={2014}, url={https://reference.wolfram.com/language/ref/ObservableModelQ.html}, note=[Accessed: 07-November-2024 ]}