PerfectNumber

PerfectNumber[n]

n 番目の完全数を与える．

詳細

  • 完全数とは，その約数の和の半分がそれ自身と等しい正の整数のことである．
  • PerfectNumber[n]では，n は正の整数でなければならない．
  • Wolfram言語の本バージョン現在，51個の完全数が発見されている．PerfectNumber[n]は任意の n について完全数を求めようと試みるが，については適当な時間内では結果を返せないと考えた方がよい．
  • PerfectNumber[n,"Even"]は n 番目の偶数の完全数を与える．Wolfram言語の本バージョン現在，最初の48個の偶数の完全数が発見されている．さらに，位置 n が定かではない3個の完全数も発見されている．PerfectNumber[n,"Even"]は 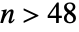について偶数の完全数を求めようとするが，適当な時間内では結果を返せないと考えた方がよい．
  • PerfectNumber[n,"Odd"]は n 番目の奇数の完全数を返そうとする．Wolfram言語の本バージョン現在奇数の完全数は発見されておらず，PerfectNumber[n,"Odd"]は結果を返せないと考えた方がよい．18番目の偶数の完全数より小さい奇数の完全数は存在しない．

例題

すべて開くすべて閉じる

例  (1)

最初の10個の完全数を返す：

スコープ  (1)

PerfectNumberは自動的にリストに縫い込まれる：

特性と関係  (4)

偶数の完全数はメルセンヌ素数指数と関係がある：

偶数の完全数はメルセンヌ素数指数と関係のある三角数である：

偶数の完全数は，メルセンヌ素数指数と関係のある六角数でもある：

6より大きい偶数の完全数はすべて，k のある値について次の形を取る：

偶数の完全数の末尾は6か28である：

最初の47個の偶数の完全数の整数長をプロットする：

考えられる問題  (2)

Wolfram言語の本バージョン現在，奇数の完全数は発見されていない：

Wolfram言語の本バージョン現在，最初の48個の偶数の完全数が発見されている：

しかし，合計51個の偶数の完全数が知られている：

Wolfram Research (2016), PerfectNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/PerfectNumber.html （2024年に更新）.

テキスト

Wolfram Research (2016), PerfectNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/PerfectNumber.html （2024年に更新）.

CMS

Wolfram Language. 2016. "PerfectNumber." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PerfectNumber.html.

APA

Wolfram Language. (2016). PerfectNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PerfectNumber.html

BibTeX

@misc{reference.wolfram_2024_perfectnumber, author="Wolfram Research", title="{PerfectNumber}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PerfectNumber.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_perfectnumber, organization={Wolfram Research}, title={PerfectNumber}, year={2024}, url={https://reference.wolfram.com/language/ref/PerfectNumber.html}, note=[Accessed: 21-November-2024 ]}