PerfectNumber

PerfectNumber[n]

给出第 n 个完全数.

更多信息

  • 完全数是一个整数，等于它所有因子的和的一半.
  • 在 PerfectNumber[n] 中，n 必须是一个正整数.
  • 在 Wolfram 语言现在的这个版本中，只有51个已知的完全数. 对于任意 n，PerfectNumber[n] 会尝试找出完全数，但如果 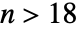，对于在合理的时间内给出结果这件事，请不要抱太大的希望,.
  • PerfectNumber[n,"Even"] 给出第 n 个偶数完全数. 截至到 Wolfram 语言的本版本为止，前48个偶完全数是已知的，还有3个的位置 n 尚不确定. PerfectNumber[n,"Even"] 将尝试得到在 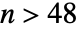时的偶数完全数，但可能不会在合理的时间内返回结果.
  • PerfectNumber[n,"Odd"] 给出第 n 个奇完全数. 在 Wolfram 语言现在的这个版本中，还不知道任何一个奇完全数，不要指望 PerfectNumber[n,"Odd"] 会返回任何结果. 没有奇完全数小于第18个偶完全数.

范例

打开所有单元关闭所有单元

基本范例  (1)

返回前 10 个完全数：

范围  (1)

PerfectNumber 自动逐项作用于列表：

属性和关系  (4)

偶完全数和 Mersenne 素数指数有关：

偶完全数是与梅森素数指数有关的三角形数：

偶完全数还是与梅森素数指数有关的六边形数：

对于 k 的某些值，所有大于 6 的偶完全数的形式如下：

偶完全数以 6 或 28 结尾：

绘制前 47 个偶完全数的整数长度：

可能存在的问题  (2)

到 Wolfram 语言现在的这个版本为止，还不知道任何一个奇完全数：

到 Wolfram 语言现在的这个版本为止，前 48 个偶完全数是已知的：

但是实际上已知的偶完全数有 51 个：

Wolfram Research (2016)，PerfectNumber，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PerfectNumber.html （更新于 2024 年）.

文本

Wolfram Research (2016)，PerfectNumber，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PerfectNumber.html （更新于 2024 年）.

CMS

Wolfram 语言. 2016. "PerfectNumber." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/PerfectNumber.html.

APA

Wolfram 语言. (2016). PerfectNumber. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PerfectNumber.html 年

BibTeX

@misc{reference.wolfram_2024_perfectnumber, author="Wolfram Research", title="{PerfectNumber}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PerfectNumber.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_perfectnumber, organization={Wolfram Research}, title={PerfectNumber}, year={2024}, url={https://reference.wolfram.com/language/ref/PerfectNumber.html}, note=[Accessed: 21-November-2024 ]}