PeronaMalikFilter

PeronaMalikFilter[image]

applies a Perona–Malik diffusion filter to image.

PeronaMalikFilter[image,t]

specifies the amount of diffusion time t to be applied.

PeronaMalikFilter[image,t,k]

uses a conductance parameter k.

PeronaMalikFilter[image,t,k,σ]

applies a Gaussian regularization of width σ to the image gradient in the conductance function.

Details

  • Perona–Malik filtering is an inhomogeneous diffusion method typically used for smoothing images while preserving edges.
  • PeronaMalikFilter works on 2D grayscale or multichannel images, operating on each channel separately.
  • PeronaMalikFilter applies the diffusion equation partial_tf=del . c_(k)(TemplateBox[{{{del , _, sigma}, f}}, Abs]) del f to every image channel .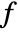
  • The function c_(k)(TemplateBox[{{{del , _, sigma}, f}}, Abs])=ⅇ^(-|del _sigmaf|^2/k^2) of the σ-regularized gradient norm TemplateBox[{{{del , _, sigma}, f}}, Abs] defines the conductance of the diffusion current. At edges where the gradient norm is large in comparison to k, diffusion is suppressed, thereby preserving edges.
  • In PeronaMalikFilter[image,t], t parameterizes the evolution of the diffusion and thereby the spatial range of the filter.
  • The conductance parameter k can take any positive value. The default value of k is Automatic, which assigns to k the 50% quantile of the gradient norm TemplateBox[{{del , f}}, Abs] of image. If more than one channel is present, the gradient norm of the channel average is taken into account.
  • The regularization parameter σ is the standard deviation of the Gaussian kernel 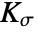, with which the image gradient 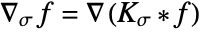is convolved. The σ-regularization makes the conductance term c_(k)(TemplateBox[{{{del , _, sigma}, f}}, Abs]) less susceptible to noise. If 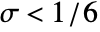, a finite difference scheme is used to determine the gradient.
  • PeronaMalikFilter[image] is equivalent to PeronaMalikFilter[image,1,Automatic,0].

Examples

open allclose all

Basic Examples  (1)

Perona–Malik filtering applied to a microscope image:

Scope  (3)

Perona–Malik filtering applied to an MRI image:

Specify a large conductance parameter to preserve only strong edges:

Specifying a minimum scale to neglect edges created by noise:

Applications  (2)

Use Perona–Malik filtering to isolate ovarian follicles in an ultrasound image:

Smooth an ultrasound image to segment an angiomyolipoma:

Properties & Relations  (1)

Normally stronger edges are enhanced and the weaker edges are blurred:

With a lower conductance parameter, blurring diminishes:

Wolfram Research (2010), PeronaMalikFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PeronaMalikFilter.html.

Text

Wolfram Research (2010), PeronaMalikFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/PeronaMalikFilter.html.

CMS

Wolfram Language. 2010. "PeronaMalikFilter." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PeronaMalikFilter.html.

APA

Wolfram Language. (2010). PeronaMalikFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PeronaMalikFilter.html

BibTeX

@misc{reference.wolfram_2024_peronamalikfilter, author="Wolfram Research", title="{PeronaMalikFilter}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PeronaMalikFilter.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_peronamalikfilter, organization={Wolfram Research}, title={PeronaMalikFilter}, year={2010}, url={https://reference.wolfram.com/language/ref/PeronaMalikFilter.html}, note=[Accessed: 21-November-2024 ]}