PositivelyOrientedPoints

PositivelyOrientedPoints[{p1,p2,p3,…,pd+1}]

检验点序列 p1,p2,p3,…,pd+1 是否为正定向.

更多信息

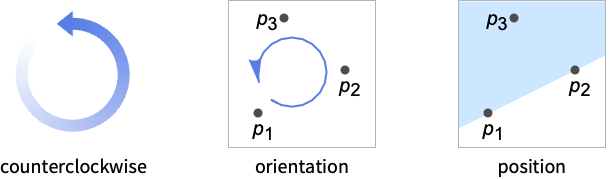
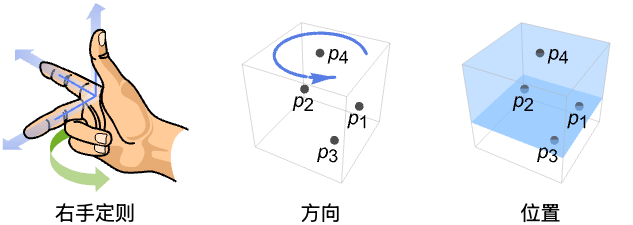
  • PositivelyOrientedPoints 在二维空间中也被称为逆时针或反时针，三维空间中也被称为右手定则.
  • 通常用于决定关于一个点集的旋转动作的方向.
  • 逆时针动作是在时钟时针移动轨迹的反方向上进行的.
  • 在二维空间中，若点 p1，p2 和 p3 的方向为逆时针，则该点序列为正定向.
  • 若点 p3 在以穿过 p1 和 p2 的直线为界且向 {-1,0} 方向延伸的半平面上，则 PositivelyOrientedPoints[{p1,p2,p3}] 给出 True.
  • 对于正定向点 p1，p2 和 p3，矩阵 {p2-p1,p3-p1} 的行列式为正.
  • 在三维空间中，如果点 p4 在以穿过 p1 且法线方向为 (p2-p1)(p3-p1) 的平面为界的半空间上，则PositivelyOrientedPoints[{p1,p2,p3,p4}] 返回 True.
  • 对于正定向点 p1，p2，p3 和 p4， p4-p1 和 (p2-p1)(p3-p1) 的点积为正.
  • 在 d 维度上，若矩阵 {p2-p1,…,pd+1-p1} 的行列式为正，则 d+1 点 p1,p2,…,pd+1 为正定向.

范例

打开所有单元关闭所有单元

基本范例  (2)

点 {0,0},{.5,-1},{1,1} 为正定向：

绘制这些点：

求点位于平面上方的条件：

范围  (3)

PositivelyOrientedPoints 适用于二维点：

三维点：

-维点：

PositivelyOrientedPoints 可处理数值坐标：

符号坐标：

用 PositivelyOrientedPoints 处理一组坐标：

点的列表：

多个点：

应用  (4)

基础应用  (2)

绘制正定向点：

显示右手定则：

几何  (2)

二维空间里，线段上的 PositivelyOrientedPoints：

等价于线段连续顶点的方向：

展示 PositivelyOrientedPoints 的鲁棒性：

属性和关系  (4)

对于共线点，PositivelyOrientedPoints 返回 False：

若为正定向，则 NegativelyOrientedPoints 返回 False：

使用 RegionMember 可检验点是否为正定向：

非正定向或非负定向的三维点为共面：

Wolfram Research (2020)，PositivelyOrientedPoints，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html.

文本

Wolfram Research (2020)，PositivelyOrientedPoints，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html.

CMS

Wolfram 语言. 2020. "PositivelyOrientedPoints." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html.

APA

Wolfram 语言. (2020). PositivelyOrientedPoints. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html 年

BibTeX

@misc{reference.wolfram_2024_positivelyorientedpoints, author="Wolfram Research", title="{PositivelyOrientedPoints}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_positivelyorientedpoints, organization={Wolfram Research}, title={PositivelyOrientedPoints}, year={2020}, url={https://reference.wolfram.com/language/ref/PositivelyOrientedPoints.html}, note=[Accessed: 21-November-2024 ]}