

HalfSpace
Details

- HalfSpace can be used as a geometric region and a graphics primitive.
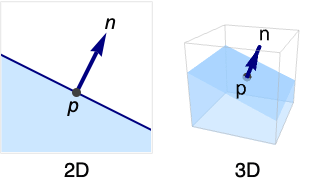
- HalfSpace corresponds to half-line or half-infinite interval in
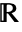 , a half-plane in
, a half-plane in 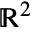 , etc.
, etc. - HalfSpace represents the set
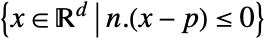 or
or 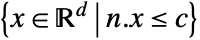 .
. - HalfSpace can be used in Graphics and Graphics3D.
- HalfSpace will be clipped by PlotRange when rendering.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, and color.
- Graphics3D rendering is affected by directives such as Opacity and color.
Examples
open all close allBasic Examples (3)
A HalfSpace in 2D:
Scope (15)
Graphics (5)
Applications (5)
Partition space in a BubbleChart:
Any convex polygon in 2D can be represented as an intersection of half-spaces:
Any convex polyhedron in 3D can be represented as an intersection of half-spaces:
Properties & Relations (7)
ClipPlanes, for a given ![]() , results in a graphic that does not render anything within the
, results in a graphic that does not render anything within the ![]() :
:
HalfSpace is a special case of ConicHullRegion:
HalfSpace is a special case of AffineHalfSpace:
HalfLine is a special case of HalfSpace:
HalfPlane is a special case of HalfSpace:
ImplicitRegion can represent any HalfSpace in ![]() :
:
ParametricRegion can represent any HalfSpace in ![]() :
:
See Also
Related Guides
History
Text
Wolfram Research (2015), HalfSpace, Wolfram Language function, https://reference.wolfram.com/language/ref/HalfSpace.html.
CMS
Wolfram Language. 2015. "HalfSpace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HalfSpace.html.
APA
Wolfram Language. (2015). HalfSpace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HalfSpace.html
BibTeX
@misc{reference.wolfram_2025_halfspace, author="Wolfram Research", title="{HalfSpace}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/HalfSpace.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_halfspace, organization={Wolfram Research}, title={HalfSpace}, year={2015}, url={https://reference.wolfram.com/language/ref/HalfSpace.html}, note=[Accessed: 23-January-2026]}