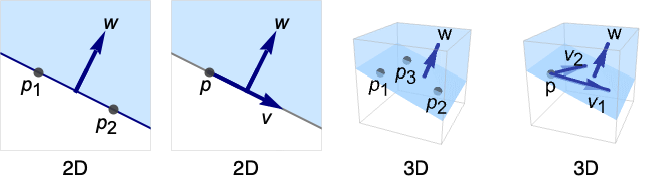
AffineHalfSpace[{p1,…,pk+1},w]
represents AffineSpace[{p1,…,pk+1}] extended in the direction w.
AffineHalfSpace[p,{v1,…,vk},w]
represents AffineSpace[p,{v1,…,vk}] extended in the direction w.


AffineHalfSpace
AffineHalfSpace[{p1,…,pk+1},w]
represents AffineSpace[{p1,…,pk+1}] extended in the direction w.
AffineHalfSpace[p,{v1,…,vk},w]
represents AffineSpace[p,{v1,…,vk}] extended in the direction w.
Details

- AffineHalfSpace can be used as a geometric region and graphics primitive.
- AffineHalfSpace represents the region
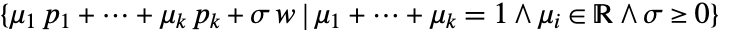 or
or 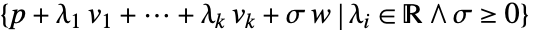 . The dimension is
. The dimension is 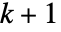 if the pi are affinely independent or the vi are linearly independent.
if the pi are affinely independent or the vi are linearly independent. - AffineHalfSpace can be used in Graphics and Graphics3D.
- AffineHalfSpace will be clipped by PlotRange when rendering.
- Graphics rendering is affected by directives such as Opacity and color as well as:
-
Thickness,Dashing 1-dimensional ( 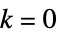 )
)FaceForm 2-dimensional (  )
) - For a two-dimensional AffineSpace, FaceForm[front,back] can be used to specify different styles for the front and back, where the front is defined to be in the direction of the normal Cross[v1,v2] or Cross[p2-p1,p3-p1], depending on which input form is used.
Examples
open all close allBasic Examples (3)
An AffineHalfSpace in 2D:
Different styles applied to an affine half-space region:
Determine if points belong to a given affine half-space region:
Scope (18)
Graphics (8)
Specification (3)
Styling (2)
Coordinates (3)
Specify coordinates by fractions of the plot range:
Specify scaled offsets from the ordinary coordinates:
Points and vectors can be Dynamic:
Regions (10)
Embedding dimension is the dimension of the coordinates:
Geometric dimension is the dimension of the region itself:
Get the conditions for membership:
An affine half-space has infinite measure and undefined centroid:
An affine half-space is unbounded:
Integrate over an affine half-space:
Applications (2)
Properties & Relations (6)
HalfLine is a special case of AffineHalfSpace:
HalfPlane is a special case of AffineHalfSpace:
HalfSpace is a special case of AffineHalfSpace:
AffineHalfSpace is a special case of ConicHullRegion:
ParametricRegion can represent any AffineHalfSpace in ![]() :
:
ImplicitRegion can represent any AffineHalfSpacein ![]() :
:
See Also
Related Guides
History
Text
Wolfram Research (2015), AffineHalfSpace, Wolfram Language function, https://reference.wolfram.com/language/ref/AffineHalfSpace.html.
CMS
Wolfram Language. 2015. "AffineHalfSpace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AffineHalfSpace.html.
APA
Wolfram Language. (2015). AffineHalfSpace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AffineHalfSpace.html
BibTeX
@misc{reference.wolfram_2025_affinehalfspace, author="Wolfram Research", title="{AffineHalfSpace}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AffineHalfSpace.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_affinehalfspace, organization={Wolfram Research}, title={AffineHalfSpace}, year={2015}, url={https://reference.wolfram.com/language/ref/AffineHalfSpace.html}, note=[Accessed: 05-February-2026]}