QHypergeometricPFQCopy to clipboard.
✖
QHypergeometricPFQ
gives the basic hypergeometric series ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
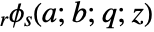 has the series expansion
has the series expansion ![sum_(k=0)^infty(TemplateBox[{{a, _, 1}, q, k}, QPochhammer]... TemplateBox[{{a, _, r}, q, k}, QPochhammer])/(TemplateBox[{{b, _, 1}, q, k}, QPochhammer]... TemplateBox[{{b, _, s}, q, k}, QPochhammer])((-1)^kq^(k (k-1)/2))^(1+s-r)(z^k)/(TemplateBox[{q, q, k}, QPochhammer]) sum_(k=0)^infty(TemplateBox[{{a, _, 1}, q, k}, QPochhammer]... TemplateBox[{{a, _, r}, q, k}, QPochhammer])/(TemplateBox[{{b, _, 1}, q, k}, QPochhammer]... TemplateBox[{{b, _, s}, q, k}, QPochhammer])((-1)^kq^(k (k-1)/2))^(1+s-r)(z^k)/(TemplateBox[{q, q, k}, QPochhammer])](Files/QHypergeometricPFQ.en/4.png) .
.- For
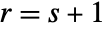 , the basic hypergeometric series is defined for
, the basic hypergeometric series is defined for 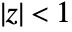 .
. - QHypergeometricPFQ automatically threads over lists. »
Examples
open allclose allBasic Examples (4)Summary of the most common use cases
https://wolfram.com/xid/0dc3vc01mxvk-ca6r73
Plot over a subset of the reals:
https://wolfram.com/xid/0dc3vc01mxvk-eew11v

Plot over a subset of the complexes:

https://wolfram.com/xid/0dc3vc01mxvk-kiedlx

Series expansion at the origin:
https://wolfram.com/xid/0dc3vc01mxvk-f65ufv

Scope (21)Survey of the scope of standard use cases
Numerical Evaluation (6)
https://wolfram.com/xid/0dc3vc01mxvk-l274ju
https://wolfram.com/xid/0dc3vc01mxvk-cksbl4
https://wolfram.com/xid/0dc3vc01mxvk-b0wt9
The precision of the output tracks the precision of the input:
https://wolfram.com/xid/0dc3vc01mxvk-y7k4a
https://wolfram.com/xid/0dc3vc01mxvk-hfml09
Evaluate efficiently at high precision:
https://wolfram.com/xid/0dc3vc01mxvk-di5gcr

https://wolfram.com/xid/0dc3vc01mxvk-bq2c6r
QHypergeometricPFQ threads elementwise over lists in its fourth argument:
https://wolfram.com/xid/0dc3vc01mxvk-bhng5j
QHypergeometricPFQ threads elementwise over sparse and structured arrays in its fourth argument:

https://wolfram.com/xid/0dc3vc01mxvk-fgz5td


https://wolfram.com/xid/0dc3vc01mxvk-d45z2i

Compute the elementwise values of an array using automatic threading:
https://wolfram.com/xid/0dc3vc01mxvk-thgd2
Or compute the matrix QHypergeometricPFQ function using MatrixFunction:
https://wolfram.com/xid/0dc3vc01mxvk-o5jpo
Specific Values (4)
https://wolfram.com/xid/0dc3vc01mxvk-jevg27
For simple parameters, QHypergeometricPFQ evaluates to simpler functions:
https://wolfram.com/xid/0dc3vc01mxvk-ih9u38
https://wolfram.com/xid/0dc3vc01mxvk-ocqx3
Find a value of x for which QHypergeometricPFQ[{1/2},{3/7},5,x]=2:
https://wolfram.com/xid/0dc3vc01mxvk-f2hrld
https://wolfram.com/xid/0dc3vc01mxvk-i5y61v

TraditionalForm formatting:
https://wolfram.com/xid/0dc3vc01mxvk-d4bwh3
Visualization (2)
Plot the QHypergeometricPFQ function:
https://wolfram.com/xid/0dc3vc01mxvk-c0x9p4

https://wolfram.com/xid/0dc3vc01mxvk-dbvuei

https://wolfram.com/xid/0dc3vc01mxvk-fn4pm8

Function Properties (7)
https://wolfram.com/xid/0dc3vc01mxvk-h5x4l2
![]() has no singularities or discontinuities:
has no singularities or discontinuities:
https://wolfram.com/xid/0dc3vc01mxvk-mdtl3h
https://wolfram.com/xid/0dc3vc01mxvk-mn5jws
![]() is neither nonincreasing nor nondecreasing:
is neither nonincreasing nor nondecreasing:
https://wolfram.com/xid/0dc3vc01mxvk-nlz7s
https://wolfram.com/xid/0dc3vc01mxvk-poz8g
https://wolfram.com/xid/0dc3vc01mxvk-ctca0g

https://wolfram.com/xid/0dc3vc01mxvk-hkqec4
https://wolfram.com/xid/0dc3vc01mxvk-hdm869

QHypergeometricPFQ is neither non-negative nor non-positive:
https://wolfram.com/xid/0dc3vc01mxvk-84dui
QHypergeometricPFQ is neither convex nor concave:
https://wolfram.com/xid/0dc3vc01mxvk-8kku21
Series Expansions (2)
Find the Taylor expansion using Series:
https://wolfram.com/xid/0dc3vc01mxvk-ewr1h8

Plots of the first three approximations around ![]() :
:

https://wolfram.com/xid/0dc3vc01mxvk-binhar

Series expansion with respect to ![]() :
:
https://wolfram.com/xid/0dc3vc01mxvk-jmafrm
Applications (8)Sample problems that can be solved with this function
Two natural ![]() -extensions of the exponential function:
-extensions of the exponential function:
https://wolfram.com/xid/0dc3vc01mxvk-f3st20
https://wolfram.com/xid/0dc3vc01mxvk-b4j5q1
https://wolfram.com/xid/0dc3vc01mxvk-bh8cc2
https://wolfram.com/xid/0dc3vc01mxvk-fvih2c
https://wolfram.com/xid/0dc3vc01mxvk-9b5oi
https://wolfram.com/xid/0dc3vc01mxvk-hzi8lj
https://wolfram.com/xid/0dc3vc01mxvk-frshd9
A ![]() -analog of the Legendre polynomial:
-analog of the Legendre polynomial:
https://wolfram.com/xid/0dc3vc01mxvk-b15hva
https://wolfram.com/xid/0dc3vc01mxvk-gw9mfs

Recover the Legendre polynomial as ![]() :
:
https://wolfram.com/xid/0dc3vc01mxvk-gs464z
https://wolfram.com/xid/0dc3vc01mxvk-bvresa
https://wolfram.com/xid/0dc3vc01mxvk-fygjyv
Compare with the usual logarithm for base ![]() :
:

https://wolfram.com/xid/0dc3vc01mxvk-hc4uit

The Lambert series ![]() can be expressed in terms of the basic hypergeometric series:
can be expressed in terms of the basic hypergeometric series:
https://wolfram.com/xid/0dc3vc01mxvk-pfwuco
Verify the identity through series expansion:
https://wolfram.com/xid/0dc3vc01mxvk-lwn5z
The Lambert series is related to the generating function for the number of divisors:
https://wolfram.com/xid/0dc3vc01mxvk-epdwvy
https://wolfram.com/xid/0dc3vc01mxvk-dypze5
Define the Stieltjes–Wigert polynomials:
https://wolfram.com/xid/0dc3vc01mxvk-ihrhzf
Generate the first few polynomials:
https://wolfram.com/xid/0dc3vc01mxvk-c878jr
Verify an alternative expression for the first few polynomials:

https://wolfram.com/xid/0dc3vc01mxvk-bh6buc
Verify the three-term recurrence relation for the first few polynomials:

https://wolfram.com/xid/0dc3vc01mxvk-i9x7xr
Verify the generating function relation for the first few polynomials:

https://wolfram.com/xid/0dc3vc01mxvk-dn6vbb
Properties & Relations (3)Properties of the function, and connections to other functions
QHypergeometricPFQ is not closed under differentiation with respect to ![]() :
:
https://wolfram.com/xid/0dc3vc01mxvk-c8xo9j
It is closed under ![]() -difference:
-difference:
https://wolfram.com/xid/0dc3vc01mxvk-bo3rgf
https://wolfram.com/xid/0dc3vc01mxvk-ew7z4c
https://wolfram.com/xid/0dc3vc01mxvk-cnre8b
https://wolfram.com/xid/0dc3vc01mxvk-bcggwg
https://wolfram.com/xid/0dc3vc01mxvk-jy81an
![]() -series are building blocks of other
-series are building blocks of other ![]() -factorial functions:
-factorial functions:
https://wolfram.com/xid/0dc3vc01mxvk-fqpimv
https://wolfram.com/xid/0dc3vc01mxvk-fhb7mj
Possible Issues (1)Common pitfalls and unexpected behavior
Some older references omit the ![]() factor in the defining series for the basic hypergeometric function. To express these in terms of QHypergeometricPFQ, add zero parameters until the condition
factor in the defining series for the basic hypergeometric function. To express these in terms of QHypergeometricPFQ, add zero parameters until the condition ![]() is satisfied. For example, a
is satisfied. For example, a ![]() function according to the old definition can be expressed in terms of
function according to the old definition can be expressed in terms of ![]() as currently defined:
as currently defined:
https://wolfram.com/xid/0dc3vc01mxvk-bchq4y

Wolfram Research (2008), QHypergeometricPFQ, Wolfram Language function, https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html (updated 2024).Text
Wolfram Research (2008), QHypergeometricPFQ, Wolfram Language function, https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html (updated 2024).
Wolfram Research (2008), QHypergeometricPFQ, Wolfram Language function, https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html (updated 2024).CMS
Wolfram Language. 2008. "QHypergeometricPFQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html.
Wolfram Language. 2008. "QHypergeometricPFQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html.APA
Wolfram Language. (2008). QHypergeometricPFQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html
Wolfram Language. (2008). QHypergeometricPFQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QHypergeometricPFQ.htmlBibTeX
@misc{reference.wolfram_2025_qhypergeometricpfq, author="Wolfram Research", title="{QHypergeometricPFQ}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html}", note=[Accessed: 04-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_qhypergeometricpfq, organization={Wolfram Research}, title={QHypergeometricPFQ}, year={2024}, url={https://reference.wolfram.com/language/ref/QHypergeometricPFQ.html}, note=[Accessed: 04-April-2025
]}