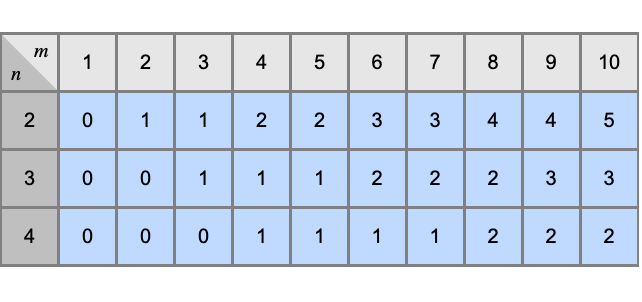
Quotient

Quotient[m,n]

n と m の整数商を与える．

Quotient[m,n,d]

オフセット d を使用する．

詳細

  • 商は比または割合としても知られている．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • Quotient[m,n]は m/n 以下の最大の整数を与える．
  • Quotient[m,n,d]は d<=m-nx<d+n となるような x を返す．

例題

すべて開くすべて閉じる

例  (2)

2つの数の商を求める：

商の列をプロットする：

スコープ  (16)

数値評価  (8)

Quotientは整数に使うことができる：

有理数：

厳密ではない実数：

厳密数：

複素数：

大きい整数について計算する：

オフセット付きで商を計算する：

Quotientは要素単位でリストに縫い込まれる：

記号演算  (8)

不等式を簡約する：

記号式を簡約する：

式を簡約する：

QuotientをFloorについて展開する：

Quotientを区分関数として表す：

積分を評価する：

再帰方程式：

母関数：

アプリケーション  (11)

基本的なアプリケーション  (6)

最初の100組の整数ペアの商の表：

2つの整数の商をプロとする：

2による除算の商をプロットする：

商をプロットする：

2つの関数の商の3Dプロットを生成する：

2つの複素変数の商をプロットする：

整数論  (5)

NestWhileListを使ってQuotientを正の引数について計算する：

以下と比較する：

除算がどのように行われるかを示す：

2か3で割り切れるが6では割り切れない1000未満の正の整数の数を数える：

直接数える：

ユークリッドアルゴリズムを実装する：

以下と比較する：

Quotientを含む式を簡約する：

特性と関係  (6)

QuotientRemainderの最初の部分はQuotientである：

Quotient[m,n]は，整数についてはFloor[m/n]に等しい：

n*Quotient[m,n,d]+Mod[m,n,d]は常に m である：

Quotient[m,n]+FractionalPart[m/n]は，正の整数については常に である：

PiecewiseExpandを使って区分関数として表す：

Quotientを含む式を簡約する：

考えられる問題  (1)

Quotientは自動的には値を簡約しない：

インタラクティブな例題  (1)

2つの整数の商をプロットする：

おもしろい例題  (2)

Quotientのフーリエ(Fourier)変換の引数をプロットする：

Quotientのウラム(Ulam)螺線をプロットする：

Wolfram Research (1988), Quotient, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quotient.html （2002年に更新）.

テキスト

Wolfram Research (1988), Quotient, Wolfram言語関数， https://reference.wolfram.com/language/ref/Quotient.html （2002年に更新）.

CMS

Wolfram Language. 1988. "Quotient." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Quotient.html.

APA

Wolfram Language. (1988). Quotient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quotient.html

BibTeX

@misc{reference.wolfram_2025_quotient, author="Wolfram Research", title="{Quotient}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Quotient.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_quotient, organization={Wolfram Research}, title={Quotient}, year={2002}, url={https://reference.wolfram.com/language/ref/Quotient.html}, note=[Accessed: 03-April-2025 ]}