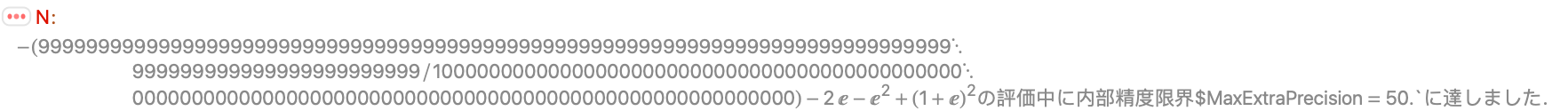RealSign

RealSign[x]

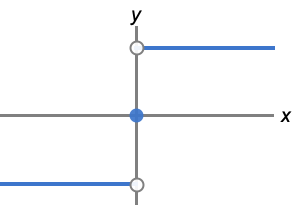
x が負か0か正かによって，-1，0あるいは1を与える．

詳細

  • RealSignはsgnあるいはsignumとしても知られている．
  • 記号操作・数値操作の両方に適した数学関数である．
  • RealSign[x]はPiecewise[{{-1,x<0},{1,x>0}}]に等しい．
  • RealSignは区分定数で，原点以外のあらゆるところで微分することができる．
  • RealSignは，記号式の符号を決定するためにさまざまな変換を試す．
  • 厳密な数量については，RealSignは内部的に数値近似を使って結果を出す．このプロセスは大域変数$MaxExtraPrecisionの設定に影響されることがある．
  • RealSignは自動的にリストに縫い込まれる． »
  • RealSignはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (4)

正の数：

負の数：

実数の部分集合上でRealSignをプロットする：

RealSignの微分：

不定積分：

スコープ  (28)

数値評価  (5)

数値的に評価する：

RealSignは，虚数については未評価のままになる：

RealSignは常に無限精度の結果を返す：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のRealSign関数を計算することもできる：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

特定の値  (5)

固定点におけるRealSignの値：

ゼロにおける値：

無限大における値：

記号的に評価する：

TemplateBox[{x}, RealSign]=0となるような の値を求める：

結果を可視化する：

可視化  (3)

TemplateBox[{{1, +, x}}, RealSign]をプロットする：

RealSignを第1引数に沿ってプロットする：

RealSignを三次元でプロットする：

関数の特性  (10)

RealSignは実数の入力についてしか定義されない：

RealSign関数の値域：

RealSignは奇関数である：

RealSignは解析関数ではない：

特異点と不連続点の両方を持つ：

RealSignは非減少である：

RealSignは単射ではない：

RealSignは全射ではない：

RealSignは非負でも非正でもない：

RealSignは凸でも凹でもない：

TraditionalFormによる表示：

微分と積分  (5)

についての一次導関数：

導関数の定義を使って同等の式を得る：

複素変数の関数Signは微分できない：

そのより高次の導関数はその一次導関数と同じである：

Integrateを使って不定積分を計算する：

定積分：

その他の積分例：

アプリケーション  (6)

RealSignを含む微分方程式を解く：

RealSignのフーリエ(Fourier)余弦級数を計算する：

RealSignを含む方程式を解く：

RealSignを含む不等式を証明する：

RealSignを含む式を簡約する：

Rademacher関数を定義する：

（垂直にシフトされた）Rademacher関数をプロットする：

単位区間の直交性をチェックする：

特性と関係  (9)

RealSign は実数についてしか定義されない：

Signは複素数について定義される：

RealSignは微分可能な関数である：

Signは微分可能ではない：

RealSignは積分可能な関数である：

Signは実数引数についてのみ積分可能である：

RealSignはベキ等元である：

FullSimplifyを使ってRealSignを含む式を簡約する：

定積分：

積分変換：

Piecewiseに変換する：

ネストをほどく：

考えられる問題  (4)

純粋に実数の引数については，RealSignは厳密な答を返す：

RealSignは，数値引数について未評価に置かれることがある：

Simplifyを使って式の符号を得る：

RealSignの機械精度数値評価は誤った結果を与えることがある：

任意精度で評価すると正しい結果が返される：

$MaxExtraPrecisionの設定をより大きくすることが必要かもしれない：

RealSignを行列に適用しても行列の符号関数は与えられない：

おもしろい例題  (3)

3符号関数の対称積で反復たたみ込み積分を作る：

一般化されたフーリエ級数を使ってRealSignを近似する：

RealSignの有理近似を計算する：

Wolfram Research (2017), RealSign, Wolfram言語関数， https://reference.wolfram.com/language/ref/RealSign.html （2021年に更新）.

テキスト

Wolfram Research (2017), RealSign, Wolfram言語関数， https://reference.wolfram.com/language/ref/RealSign.html （2021年に更新）.

CMS

Wolfram Language. 2017. "RealSign." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/RealSign.html.

APA

Wolfram Language. (2017). RealSign. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RealSign.html

BibTeX

@misc{reference.wolfram_2024_realsign, author="Wolfram Research", title="{RealSign}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/RealSign.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_realsign, organization={Wolfram Research}, title={RealSign}, year={2021}, url={https://reference.wolfram.com/language/ref/RealSign.html}, note=[Accessed: 05-November-2024 ]}