RegionMember

RegionMember[reg,{x,y,…}]

数値の点{x,y,…}が定常領域 reg に帰属する場合はTrueを，それ以外の場合はFalse を与える．

RegionMember[reg,{x,y,…}]

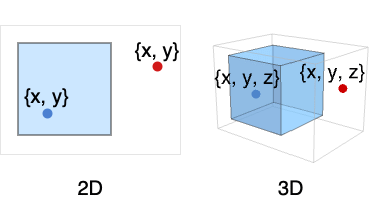
点{x,y,…}の reg への帰属条件を与える．

RegionMember[reg]

異なる点に繰り返し適用可能なRegionMemberFunction[…]を返す．

詳細

  • RegionMemberは，領域判定，帰属判定，および帰属条件における点としても知られている．
  • 定常領域とはConstantRegionQ[reg]がTrueを与える領域のことである．

例題

すべて開くすべて閉じる

例  (3)

特定の点が領域に含まれるかどうかの検定を行う：

点の帰属条件を得る：

RegionMemberFunctionを作って異なる点に適用する：

スコープ  (21)

基本的な用法  (4)

点が領域に含まれるかどうかを直接検定する：

点のリストが領域に含まれるかどうかを直接検定する：

変数{x,y}を使って点の帰属条件を得る：

RegionMemberFunctionを作って異なる点に適用する：

特別な領域  (6)

における領域：

における領域：

の領域帰属を可視化する：

領域の境界を得る：

この領域の境界ボックス上で一様にサンプルを取る：

における領域：

における領域帰属を可視化する：

における領域：

数式定義領域  (3)

陰的領域：

における領域帰属を可視化する：

領域の境界を得る：

この領域の境界ボックス上で一様にサンプルを取る：

パラメトリック領域：

メッシュ領域  (4)

2DにおけるMeshRegion：

3Dにおけるメッシュ領域：

2DにおけるBoundaryMeshRegion：

3DにおけるBoundaryMeshRegion：

派生領域  (4)

2つの領域のRegionIntersection：

領域の境界を得る：

この領域の境界ボックス上で一様にサンプルを取る：

次元混合領域のRegionUnion：

TransformedRegion：

RegionBoundary：

アプリケーション  (6)

基本  (2)

指定された国についての多角形データをMeshRegionに変換する：

都市の帰属を決定する：

RegionMemberは，パラメータ化された領域について，指定された点がどのような場合に帰属するかというパラメータについての条件を与える：

領域が点を含む例を求める：

これを可視化する：

領域内のランダムな点  (2)

点の一様集合をフィルタにかけることで，領域上に点を生成する：

領域の境界を得る：

領域の境界ボックス上で一様にサンプルを取る：

帰属点を選択する：

帰属点を可視化する：

指定された国の多角形データをMeshRegionに変換する：

領域の境界を得る：

領域の境界ボックス上で一様にサンプルを取る：

モンテカルロ積分  (2)

単位円板の面積を推定するために，モンテカルロ積分を行う：

領域の境界を得る：

領域の境界ボックス上で一様にサンプルを取る：

領域内のサンプル数を数える：

サンプル点の総数に対する領域内のサンプル数の割合を得る：

境界面積を得る：

領域面積の近似値を得る：

領域内のランダムな点を使ってモンテカルロ積分を行う：

各サンプル点で関数を評価し，その平均を取る：

厳密値と比較する：

特性と関係  (5)

Elementを使って，定常領域についての帰属判定を行うことができる：

RegionDistanceは，帰属については0である：

SignedRegionDistanceは，帰属について正ではない：

SignedRegionDistanceは，非帰属について正である：

RegionNearestを使って最も近くの帰属点を求める：

これを可視化する：

FindInstanceを使って特別な領域と数式定義領域の例を複数求める：

両方の領域に含まれる点を求める：

Wolfram Research (2014), RegionMember, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMember.html.

テキスト

Wolfram Research (2014), RegionMember, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMember.html.

CMS

Wolfram Language. 2014. "RegionMember." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionMember.html.

APA

Wolfram Language. (2014). RegionMember. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionMember.html

BibTeX

@misc{reference.wolfram_2024_regionmember, author="Wolfram Research", title="{RegionMember}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionMember.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionmember, organization={Wolfram Research}, title={RegionMember}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionMember.html}, note=[Accessed: 18-November-2024 ]}