WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

RegionProduct[reg1,reg2]

領域 reg1と reg2の直積を表す．

RegionProduct[reg1,reg2,…]

領域 reg1，reg2，…の直積を表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数式定義領域  
メッシュ領域  
アプリケーション  
特性と関係  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

RegionProduct

RegionProduct[reg1,reg2]

領域 reg1と reg2の直積を表す．

RegionProduct[reg1,reg2,…]

領域 reg1，reg2，…の直積を表す．

詳細

  • RegionProductは，外積領域としても知られている．
  • RegionProduct[reg1,reg2]は，領域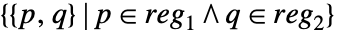を表す．
  • 積領域の埋込み次元は埋込み次元の和であり，幾何次元は幾何次元の和である．

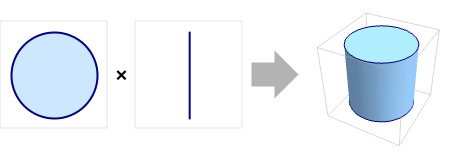
例題

すべて開く すべて閉じる

例  (3)

2本の線分の積：

Wolfram Language code: ℛ = RegionProduct[Line[{{0}, {1}}], Line[{{0}, {1}}]];
Wolfram Language code: RegionMeasure[ℛ]

可視化する：

Wolfram Language code: Region[ℛ]

円板と線分の積：

Wolfram Language code: ℛ = RegionProduct[Disk[{0, 0}, 1], Line[{{0}, {1}}]];
Wolfram Language code: RegionMeasure[ℛ]

可視化する：

Wolfram Language code: Region[ℛ]

2つのBoundaryMeshRegionオブジェクトの積：

Wolfram Language code: bmr1 = BoundaryMeshRegion[{{0, 0}, {1, 0}, {1, 1}, {0, 1}}, Line[{1, 2, 3, 4, 1}]]; bmr2 = BoundaryMeshRegion[{{0}, {1}}, Point[{{1}, {2}}]]; ℛ = RegionProduct[bmr1, bmr2]

スコープ  (7)

数式定義領域  (3)

1DにおけるImplicitRegionとParametricRegionの積：

Wolfram Language code: ℛ1 = ImplicitRegion[0 ≤ x ≤ 3, {x}]; ℛ2 = ParametricRegion[{t}, {{t, 0, 3}}]; ℛ = RegionProduct[ℛ1, ℛ2];

そのAreaを計算する：

Wolfram Language code: Area[ℛ]

これを可視化する：

Wolfram Language code: Region[ℛ]

2つのImplicitRegionオブジェクトの積：

Wolfram Language code: ℛ1 = ImplicitRegion[y ≥ x ^ 2, {x, y}]; ℛ2 = ImplicitRegion[1 ≤ x ≤ 2, {x}]; ℛ = RegionProduct[ℛ1, ℛ2];

この領域は非有界であるので，体積は不定である：

Wolfram Language code: BoundedRegionQ[ℛ]
Wolfram Language code: Volume[ℛ]

2つのParametricRegionオブジェクトの積：

Wolfram Language code: ℛ1 = ParametricRegion[{r Cos[θ], r Sin[θ]}, {{r, 0, 1}, {θ, 0, 2π}}]; ℛ2 = ParametricRegion[{t}, {{t, 0, 1}}]; ℛ = RegionProduct[ℛ1, ℛ2];

そのVolumeを計算する：

Wolfram Language code: Volume[ℛ]

メッシュ領域  (4)

1Dにおける2つのBoundaryMeshRegionオブジェクトの積：

Wolfram Language code: mr1 = BoundaryMeshRegion[{{0}, {1}}, Point[{1, 2}]]; mr2 = BoundaryMeshRegion[{{0}, {1}}, Point[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]

結果はMeshRegionであって，BoundaryMeshRegionではない：

Wolfram Language code: {MeshRegionQ[ℛ], BoundaryMeshRegionQ[ℛ]}

1Dにおける2つのMeshRegionオブジェクトの積：

Wolfram Language code: mr1 = MeshRegion[{{0}, {1}, {2}, {3}}, Line[{{1, 2}, {3, 4}}]]; mr2 = MeshRegion[{{0}, {1}}, Line[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]

Areaを計算する：

Wolfram Language code: Area[ℛ]

1Dおよび2DのBoundaryMeshRegionオブジェクトの積：

Wolfram Language code: mr1 = ConvexHullMesh[RandomReal[2, {10, 2}]]; mr2 = BoundaryMeshRegion[{{0}, {1}}, Point[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]

Volumeを計算する：

Wolfram Language code: Volume[ℛ]

1Dおよび2DのMeshRegionオブジェクトの積：

Wolfram Language code: mr1 = DelaunayMesh[RandomReal[2, {10, 2}]]; mr2 = MeshRegion[{{0}, {1}}, Line[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]

Volumeを計算する：

Wolfram Language code: Volume[ℛ]

アプリケーション  (2)

テンソル積メッシュをいくつかの1Dメッシュの積として定義する：

Wolfram Language code: pointsToMesh[data_] := MeshRegion[Transpose[{data}], Line@Table[{i, i + 1}, {i, Length[data] - 1}]];

点のリストから1Dメッシュを定義する：

Wolfram Language code: data = Table[Exp[x], {x, 0., 2, 0.1}];
Wolfram Language code: r1 = pointsToMesh[data]

2Dテンソル積メッシュを定義する：

Wolfram Language code: RegionProduct[r1, r1]

3Dテンソル積メッシュを定義する：

Wolfram Language code: RegionProduct[r1, r1, r1]

カントール(Cantor)集合の段階を表すMeshRegionを直接構築する．この集合は，区間{0,1}から始めて，各段階で中央の1/3を取り除くことで定義できる：

Wolfram Language code: cantor = {a_, b_} :> {{a, a + (b - a) / 3}, {a + (b - a)2 / 3, b}};
Wolfram Language code: CantorRegion[n_Integer ? NonNegative] := Module[{ints}, ints = Nest[Flatten[Map[Function[s, s /. cantor], #], 1]&, {{0, 1}}, n]; MeshRegion[Transpose[{Flatten[ints]}], Line@Table[{i, i + 1}, {i, 1, Length[ints]2, 2}], MeshCellStyle -> {{0, _} -> Directive[StandardGray, PointSize[Medium]], {1, _} -> Directive[Thick, Orange]}]]

最初の数段階：

Wolfram Language code: CantorRegion[0]
Wolfram Language code: CantorRegion[1]
Wolfram Language code: CantorRegion[3]

RegionProductを使ってカントールの塵を作る：

Wolfram Language code: CantorDust[k_, n_] := RegionProduct@@Table[CantorRegion[k], {n}]
Wolfram Language code: Table[CantorDust[k, 2], {k, 3}]
Wolfram Language code: Table[CantorDust[k, 3], {k, 3}]

各段階におけるカントール集合の長さを求める：

Wolfram Language code: Table[RegionMeasure[CantorRegion[k]], {k, 5}]//Rationalize

一般的公式を推理する：

Wolfram Language code: FindSequenceFunction[%, n]

2Dの各段階におけるカントールの測度を求める：

Wolfram Language code: Table[RegionMeasure[CantorDust[k, 2]], {k, 5}]//Rationalize
Wolfram Language code: FindSequenceFunction[%, n]

2Dの各段階におけるカントールの塵の測度を求める：

Wolfram Language code: Table[{k, RegionMeasure[CantorDust[k, 3]]}, {k, 0, 3}]//Rationalize
Wolfram Language code: FindSequenceFunction[%, n]

特性と関係  (10)

積のRegionEmbeddingDimensionは，入力埋込み次元の総和である：

Wolfram Language code: mr1 = MeshRegion[Tuples[{0, 1, 2, 3}, 2], Point[Range[16]]]; mr2 = MeshRegion[{{0}, {1}}, Line[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]
Wolfram Language code: RegionEmbeddingDimension[ℛ] == RegionEmbeddingDimension[mr1] + RegionEmbeddingDimension[mr2]

積のRegionDimensionは，入力次元の総和である：

Wolfram Language code: ℛ1 = Disk[]; ℛ2 = Line[{{0}, {1}}]; ℛ = RegionProduct[ℛ1, ℛ2];
Wolfram Language code: RegionDimension[ℛ] == RegionDimension[ℛ1] + RegionDimension[ℛ2]

特殊な領域のRegionProductは，未評価のまま残される：

Wolfram Language code: ℛ = RegionProduct[Disk[], Line[{{0}, {1}}]]

これは領域であり，計算に使うことができる：

Wolfram Language code: RegionQ[ℛ]
Wolfram Language code: {RegionMeasure[ℛ], RegionCentroid[ℛ]}

数式定義領域のRegionProductは，未評価のまま残される：

Wolfram Language code: ℛ1 = ImplicitRegion[x ^ 2 + y ^ 2 ≤ 1, {x, y}]; ℛ = RegionProduct[ℛ1, ℛ1]

これは領域であり，計算に使うことができる：

Wolfram Language code: RegionQ[ℛ]
Wolfram Language code: {RegionMeasure[ℛ], RegionCentroid[ℛ]}

MeshRegionオブジェクあるいはBoundaryMeshRegionオブジェクトの積は，それ自身がMeshRegionである：

Wolfram Language code: mr1 = DelaunayMesh[RandomReal[2, {10, 2}]]; mr2 = BoundaryMeshRegion[{{0}, {1}}, Point[{1, 2}]]; ℛ = RegionProduct[mr1, mr2]
Wolfram Language code: MeshRegionQ[ℛ]

積のRegionMeasureは，入力測度の積である：

Wolfram Language code: ℛ1 = Disk[{0, 0}, {3, 2}, {π / 4, 3π / 4}]; ℛ2 = Line[{{0}, {2}}]; ℛ = RegionProduct[ℛ1, ℛ2];
Wolfram Language code: RegionMeasure[ℛ] == RegionMeasure[ℛ1]RegionMeasure[ℛ2]

積のRegionCentroidは，入力の重心を結合したものである：

Wolfram Language code: ℛ1 = Disk[{0, 0}, {3, 2}, {π / 4, 3π / 4}]; ℛ2 = Line[{{0}, {2}}]; ℛ = RegionProduct[ℛ1, ℛ2];
Wolfram Language code: RegionCentroid[ℛ] == Join[RegionCentroid[ℛ1], RegionCentroid[ℛ2]]

Rectangleは2つのLineオブジェクトの積である：

Wolfram Language code: ℛ1 = RegionProduct[Line[{{0}, {2}}], Line[{{0}, {1}}]]; ℛ2 = Rectangle[{0, 0}, {2, 1}];
Wolfram Language code: {Region[ℛ1], Region[ℛ2]}

帰属が等しいことを示す：

Wolfram Language code: RegionEqual[ℛ1, ℛ2]

Cuboidは3つのLineオブジェクトの積である：

Wolfram Language code: ℛ1 = RegionProduct[Line[{{0}, {3}}], Line[{{0}, {2}}], Line[{{0}, {1}}]]; ℛ2 = Cuboid[{0, 0, 0}, {3, 2, 1}];
Wolfram Language code: {Region[ℛ1], Region[ℛ2]}

帰属が等しいことを示す：

Wolfram Language code: RegionEqual[ℛ1, ℛ2]

CylinderはDiskとLineの積である：

Wolfram Language code: ℛ1 = RegionProduct[Disk[{0, 0}, 2], Line[{{0}, {1}}]]; ℛ2 = Cylinder[{{0, 0, 0}, {0, 0, 1}}, 2];
Wolfram Language code: {Region[ℛ1], Region[ℛ2]}

帰属が等しいことを示す：

Wolfram Language code: RegionEqual[ℛ1, ℛ2]

おもしろい例題  (1)

カントールの塵のような領域をカントール集合の積として定義する：

Wolfram Language code: cantor = {a_, b_} :> {{a, a + (b - a) / 3}, {a + (b - a)2 / 3, b}};
Wolfram Language code: CantorRegion[n_Integer ? NonNegative] := Module[{ints}, ints = Nest[Flatten[Map[Function[s, s /. cantor], #], 1]&, {{0, 1}}, n]; MeshRegion[Transpose[{Flatten[ints]}], Line@Table[{i, i + 1}, {i, 1, Length[ints]2, 2}]]]
Wolfram Language code: CantorDust[n_List] := RegionProduct@@(CantorRegion /@ n)

2Dにおけるカントール集合の積：

Wolfram Language code: Table[CantorDust[{i, j}], {i, 0, 3}, {j, 0, 3}]//GraphicsGrid

3Dにおけるカントール集合の積：

Wolfram Language code: Table[CantorDust[{i, j, k}], {i, 1, 3}, {j, 1, 2}, {k, 1, 2}]
Wolfram Research (2014), RegionProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionProduct.html.

テキスト

Wolfram Research (2014), RegionProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionProduct.html.

CMS

Wolfram Language. 2014. "RegionProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionProduct.html.

APA

Wolfram Language. (2014). RegionProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionProduct.html

BibTeX

@misc{reference.wolfram_2026_regionproduct, author="Wolfram Research", title="{RegionProduct}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionProduct.html}", note=[Accessed: 06-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_regionproduct, organization={Wolfram Research}, title={RegionProduct}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionProduct.html}, note=[Accessed: 06-November-2026]}