Search for all pages containing RegionProduct
RegionProduct[reg1,reg2]
represents the Cartesian product of the regions reg1 and reg2.
RegionProduct[reg1,reg2,…]
represents the Cartesian product of the regions reg1, reg2, ….


RegionProduct
RegionProduct[reg1,reg2]
represents the Cartesian product of the regions reg1 and reg2.
RegionProduct[reg1,reg2,…]
represents the Cartesian product of the regions reg1, reg2, ….
Details
- RegionProduct is also known as outer product region.
- RegionProduct[reg1,reg2] represents the region
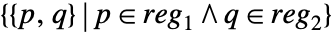 .
. - The embedding dimension of the product region is the sum of embedding dimensions, and the geometric dimension is the sum of geometric dimensions.
Examples
open all close allBasic Examples (3)
The product of two line segments:
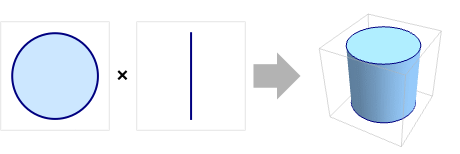
The product of a disk and a line segment:
The product of two BoundaryMeshRegion objects:
Scope (7)
Formula Regions (3)
A product of an ImplicitRegion and a ParametricRegion in 1D:
Compute its Area:
A product of two ImplicitRegion objects:
The region is unbounded, so its volume is infinite:
A product of two ParametricRegion objects:
Compute its Volume:
Mesh Regions (4)
A product of two BoundaryMeshRegion objects in 1D:
The result is a MeshRegion, not a BoundaryMeshRegion:
A product of two MeshRegion objects in 1D:
Compute the Area:
A product of 1D and 2D BoundaryMeshRegion objects:
Compute the Volume:
A product of 1D and 2D MeshRegion objects:
Compute the Volume:
Applications (2)
Define a tensor product mesh as the product of several 1D meshes:
Define a 1D mesh from a list of points:
Define a 2D tensor product mesh:
Define a 3D tensor product mesh:
Directly construct a MeshRegion representing a stage for the Cantor set. The set is defined by starting with the interval {0,1} and at each step removing the middle third:
Use RegionProduct to produce Cantor dust:
Find the length of the Cantor set at each stage:
Properties & Relations (10)
The RegionEmbeddingDimension of a product is the sum of input embedding dimensions:
The RegionDimension of a product is the sum of input dimensions:
A RegionProduct of special regions is left unevaluated:
It is a region and can be used for computation:
A RegionProduct of formula regions is left unevaluated:
It is a region and can be used for computation:
A product of MeshRegion or BoundaryMeshRegion objects is itself a MeshRegion:
The RegionMeasure of a product is the product of the input measures:
The RegionCentroid of a product is the input centroids joined together:
A Rectangle is a product of two Line objects:
Show membership is equivalent:
A Cuboid is a product of three Line objects:
Show membership is equivalent:
Related Guides
History
Text
Wolfram Research (2014), RegionProduct, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionProduct.html.
CMS
Wolfram Language. 2014. "RegionProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionProduct.html.
APA
Wolfram Language. (2014). RegionProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionProduct.html
BibTeX
@misc{reference.wolfram_2025_regionproduct, author="Wolfram Research", title="{RegionProduct}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionProduct.html}", note=[Accessed: 24-November-2025]}
BibLaTeX
@online{reference.wolfram_2025_regionproduct, organization={Wolfram Research}, title={RegionProduct}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionProduct.html}, note=[Accessed: 24-November-2025]}