SolidAngle

SolidAngle[p,{u1,…,ud}]

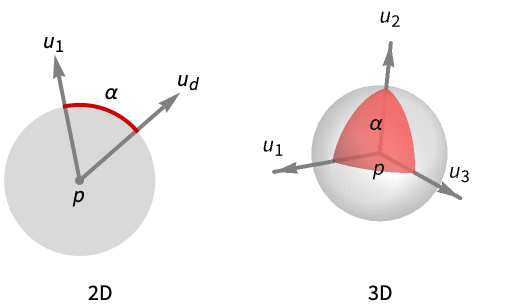
gives the solid angle at the point p and spanned by the vectors u1,…,ud.

SolidAngle[p,reg]

gives the solid angle subtended by the region reg.

Details

  • SolidAngle is also known as planar angle or spherical angle.
  • SolidAngle is typically used to measure the amount of the field of view from a point that an object covers.
  • SolidAngle[p,{u1,…,ud}] is the measure of the intersection of the d-dimensional unit sphere Sphere[p] and the conic hull generated by the vectors u1,…,ud.
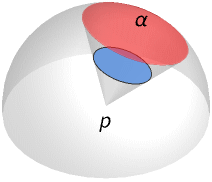
  • SolidAngle[p,reg] is the measure of the intersection of the unit sphere centered at p and half‐lines from p through points of the region reg.

Examples

open allclose all

Basic Examples  (1)

The solid angle at the point {1/2,1/2,0} and spanned by the vectors {0,0,1}, {0,1,1}, {1,1,1} and {1,0,1}:

Scope  (2)

Use SolidAngle to find the angle at the point and spanned by the vectors:

The solid angle subtended by the Cone[{{1,1,1},{0,0,0}}]:

Properties & Relations  (5)

SolidAngle[{0,0},{u1,u2}] is the planar angle between the half‐lines from the point p in the direction of u1 and u2:

SolidAngle[{0,0,0},{u1,u2,u3}] is the surface area of the triangle on the unit sphere with corner points :

In 2D, SolidAngle[p,Line[{q1,q2}] is equivalent to PlanarAngle[{q1,p,q2}]:

In 3D, SolidAngle[p,reg] is the surface area of the intersection of the unit sphere centered at p that lies in the infinite cone with vertex p and enclosing reg:

SolidAngle[p,{u1,…,ud}] is equivalent to PolyhedronAngle[ℛ,p], where u1,…,ud are vectors adjacent to the point p in a polyhedron ℛ:

Wolfram Research (2019), SolidAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/SolidAngle.html.

Text

Wolfram Research (2019), SolidAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/SolidAngle.html.

CMS

Wolfram Language. 2019. "SolidAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SolidAngle.html.

APA

Wolfram Language. (2019). SolidAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SolidAngle.html

BibTeX

@misc{reference.wolfram_2024_solidangle, author="Wolfram Research", title="{SolidAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/SolidAngle.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_solidangle, organization={Wolfram Research}, title={SolidAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/SolidAngle.html}, note=[Accessed: 21-November-2024 ]}