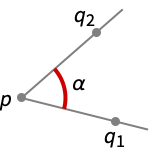
PlanarAngle[p{q1,q2}]
gives the angle between the half‐lines from p through q1 and q2.
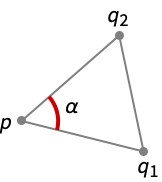
PlanarAngle[{q1,p,q2}]
gives the angle at p formed by the triangle with vertex points p, q1 and q2.
PlanarAngle[…,"spec"]
gives the angle specified by "spec".


PlanarAngle
PlanarAngle[p{q1,q2}]
gives the angle between the half‐lines from p through q1 and q2.
PlanarAngle[{q1,p,q2}]
gives the angle at p formed by the triangle with vertex points p, q1 and q2.
PlanarAngle[…,"spec"]
gives the angle specified by "spec".
Details



- PlanarAngle is also known as angle.
- PlanarAngle[p{q1,q2}] gives the length of the arc of the unit circle Circle[p] delimited by the half-line from p through q1 on the left and the half-line from p to q2 on the right.
- Two half‐lines from p through q1 and q2 delimit two angles α1 and α2 at p.
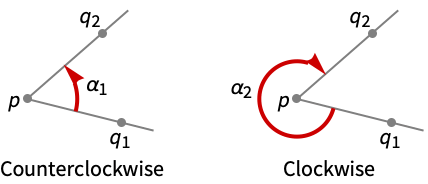
- The following specifications "spec" can be given:
-
"Counterclockwise" angle formed by the counterclockwise rotation from q1 to q2 "Clockwise" angle formed by the clockwise rotation from q1 to q2 - PlanarAngle[p{q1,q2},"Counterclockwise"] is equivalent to PlanarAngle[p{q1,q2}].
- PlanarAngle[p{q1,q2},"Clockwise"] is equivalent to PlanarAngle[p{q2,q1}].
- PlanarAngle[{q1,p,q2}] is the angle subtended by the line segment q1 q2 from p.
- The triangle with vertex points q1, p and q2 defines three angles α1, α2 and α3 at p.
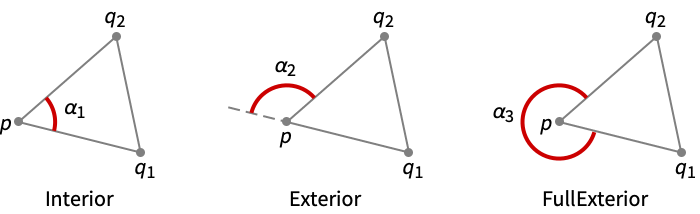
- The following specifications "spec" can be given:
-
"Interior" interior (inside) angle of the triangle at p "Exterior" exterior angle of the triangle at p "FullExterior" full exterior angle of the triangle at p - PlanarAngle[{q1,p,q2},"Interior"] is equivalent to PlanarAngle[{q1,p,q2}].
- PlanarAngle[{q1,p,q2},"Exterior"] is equivalent to π-PlanarAngle[{q1,p,q2}].
- PlanarAngle[{q1,p,q2},"FullExterior"] is equivalent to 2π-PlanarAngle[{q1,p,q2}].
- With the specification "Interior", "Exterior" or "FullExterior", PlanarAngle[p{q1,q2},"spec"] is taken to be PlanarAngle[{q1,p,q2},"spec"].
- With the specification "Counterclockwise" or "Clockwise", PlanarAngle[{q1,p,q2},"spec"] is taken to be PlanarAngle[p{q1,q2}, "spec"].
- PlanarAngle can be used with symbolic points in GeometricScene.
Examples
open all close allBasic Examples (2)
Scope (7)
Basic Uses (2)
Use PlanarAngle to find the angle between two half‐lines:
PlanarAngle works with numeric arguments:
Specifications (5)
Applications (6)
Find the interior angle of a triangle at a point p:
An AASTriangle:
Properties & Relations (7)
PlanarAngle[p,{q2,q1}] is equal to 2π-PlanarAngle[p,{q1,q2}]:
PlanarAngle[{q1,p,q2},"Interior"] is the smallest angle formed by the rotations around p:
PlanarAngle[p{q1,q2}] takes values from 0 to 2π:
PlanarAngle[{q1,p,q2}] takes values from 0 to π:
Dihedral angle is the planar angle in the plane defined by the normal p2-p1 and a point p1:
PlanarAngle[p->{q1,q2}] is equivalent to PolygonAngle[ℛ, p] where q1 and q2 are adjacent points of p in a polygon ℛ:
PlanarAngle[{q1,p,q2}] is equivalent to SolidAngle[p,{q1,q2}]:
Possible Issues (1)
PlanarAngle gives generic values for symbolic parameters:
See Also
VectorAngle SolidAngle DihedralAngle PolygonAngle PolyhedronAngle Dot AnglePath AngleBisector GeometricScene
Function Repository: AngleBetweenPlanes VertexArc
Related Guides
History
Text
Wolfram Research (2019), PlanarAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/PlanarAngle.html.
CMS
Wolfram Language. 2019. "PlanarAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PlanarAngle.html.
APA
Wolfram Language. (2019). PlanarAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PlanarAngle.html
BibTeX
@misc{reference.wolfram_2025_planarangle, author="Wolfram Research", title="{PlanarAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/PlanarAngle.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_planarangle, organization={Wolfram Research}, title={PlanarAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/PlanarAngle.html}, note=[Accessed: 03-March-2026]}