SphericalShell
SphericalShell[c,{rinner,router}]
c を中心とした,内半径 rinner,外半径 routerの塗り潰された球体殻を表す.
詳細とオプション

- SphericalShellは,幾何学領域およびグラフィックスプリミティブとして使うことができる.
- SphericalShell[]はSphericalShell[{0,0,0},{1/2,1}]に等しい.
- SphericalShell[r]はSphericalShell[{0,0,0},{r/2,r}]に等しい.
- SphericalShell[{rinner,router}]はSphericalShell[{0,0,0},{rinner,router}]に等しい.
- SphericalShellは,塗り潰された球体殻
![{x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)} {x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)}](Files/SphericalShell.ja/2.png) を表す.この領域は,長さ
を表す.この領域は,長さ 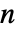 の点 c について
の点 c について 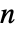 次元である.
次元である. - SphericalShellでは,c は
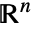 内で
内で である任意の点でよい.
である任意の点でよい. - SphericalShellはGraphicsおよびGraphics3Dで使うことができる.
- グラフィックスでは,点 c と半径 r はDynamic式でよい.
- グラフィックスの描画は,FaceForm,EdgeForm,Specularity,Opacity,色等の指示子の影響を受ける.

例題
すべて開くすべて閉じるスコープ (20)
グラフィックス (10)
アプリケーション (5)
標準的なピンポン球の球体殻の質量は2.7グラムで外半径は40mmである:
これは密度![]() のセルロイドでできている.
のセルロイドでできている.![]() であるので,ピンポン球の内半径を求めることができる:
であるので,ピンポン球の内半径を求めることができる:
かつて,宇宙は同心円の天球からなると信じられていた.宇宙の中心は地球で,その周りに惑星の球殻と太陽があるのである.惑星と太陽の順番については意見が分かれていた.プラトンとプトレマイオスの球殻の並べ順は異なっている:
ラベル付きの球殻集合を使ってこの2人の哲学者が描く宇宙を可視化し比較することができる:
真珠は,軟体動物によって層ごとに形成される.真珠の光学的特性は,不透明な表層だけでなく,多くの半透明な層からの反射光に由来する.不透明度が異なるネストした球殻の2つの集合を比較することで,半透明な層が生み出す差を見ることができる:
ゴルフボールには複数の層がある.外側はくぼみのある殻であり,その内側に1つあるいは複数の層がある.外側の層を球殻とボールの集合の間のRegionDifferenceとしてモデル化する.くぼみの分布を球のメッシュのMeshCoordinatesを使って得る:
内側を見るために外側を取り去るために,区間上でこの領域を離散化する:
最後に,ゴルフボールの内部殻(中心からのオフセット)のためのボールを作って層を視覚的に分離する:
風船は,球体殻として近似することができる.風船が10単位の材料からできていると仮定する.厚さが風船の外半径にどのように依存するかを求める:
特性と関係 (4)
Ballは,![]() が0に近付く際のSphericalShellの極限である:
が0に近付く際のSphericalShellの極限である:
Sphereは,![]() が
が ![]() に近付く際のSphericalShellの極限である:
に近付く際のSphericalShellの極限である:
SphericalShellは,2つの同心Ball領域間のRegionDifferenceの閉包である:
SphericalShellは,半径![]() の球から
の球から![]() より近いすべての点である:
より近いすべての点である:
テキスト
Wolfram Research (2015), SphericalShell, Wolfram言語関数, https://reference.wolfram.com/language/ref/SphericalShell.html.
CMS
Wolfram Language. 2015. "SphericalShell." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalShell.html.
APA
Wolfram Language. (2015). SphericalShell. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SphericalShell.html