SphericalShell[c,{rinner,router}]
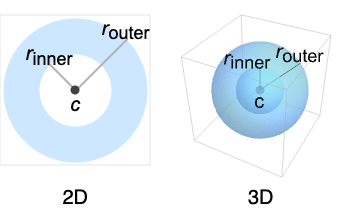
代表一个球心在 c ,内半径为 rinner 且外半径为 router 的填充球壳.


SphericalShell
SphericalShell[c,{rinner,router}]
代表一个球心在 c ,内半径为 rinner 且外半径为 router 的填充球壳.
更多信息和选项

- SphericalShell 可被用作几何区域和图形基元.
- SphericalShell[] 等价于 SphericalShell[{0,0,0},{1/2,1}].
- SphericalShell[r] 等价于 SphericalShell[{0,0,0},{r/2,r}].
- SphericalShell[{rinner,router}] 等价于 SphericalShell[{0,0,0},{rinner,router}].
- SphericalShell 代表一个填充球壳
![{x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)} {x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)}](Files/SphericalShell.zh/2.png) . 这个区域对长度为
. 这个区域对长度为 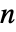 的点 c 是
的点 c 是 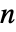 维的.
维的. - SphericalShell 允许 c 为
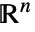 中的任意一点,且有
中的任意一点,且有 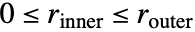 .
. - SphericalShell 可用于 Graphics 和 Graphics3D 中.
- 在图形中,点 c 和半径 r 可以是 Dynamic 表达式.
- 有些指令,比如 FaceForm、EdgeForm、Specularity、Opacity 和着色会影响图形渲染.
范例
打开所有单元 关闭所有单元范围 (20)
图形 (10)
应用 (5)
人们曾经相信宇宙是一个同心的天球系统. 宇宙的中心是地球,外面是包括行星和太阳的球壳. 关于行星和太阳的准确次序存在着争议. 柏拉图和托勒密对天球进行了不同的排序:
珍珠是软体动物的产物,一层套一层. 珍珠的光学特性来自光线在许多半透明层的反射,而不是只有一层不透明的表面. 可以构建两套相互嵌套的、透明度不同的球壳来查看半透明层所产生的不同效果:
高尔夫球有很多层,外层、凹痕层、一个或更多内层. 用球壳和一组球的 RegionDifference 来模拟外层. 利用球的网格的 MeshCoordinates 来获得凹痕的分布:
最后,画出高尔夫球的内核,稍稍偏离中心,使我们能同时看到各层结构:
可以用球壳来近似模拟一个气球. 假设气球是由10个单位的某种材料构成的,求气球的厚度和外半径之间的关系:
属性和关系 (4)
Ball 是 SphericalShell 在 ![]() 接近0时的极限情况:
接近0时的极限情况:
Sphere 是 SphericalShell 在 ![]() 接近
接近 ![]() 时的极限情况:
时的极限情况:
SphericalShell 是两个同心 Ball 区域之间 RegionDifference 的封闭外包:
SphericalShell 距半径为 ![]() 的球面距离小于
的球面距离小于 ![]() 的所有点:
的所有点:
相关指南
-
▪
- 基本几何区域
文本
Wolfram Research (2015),SphericalShell,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SphericalShell.html.
CMS
Wolfram 语言. 2015. "SphericalShell." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalShell.html.
APA
Wolfram 语言. (2015). SphericalShell. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SphericalShell.html 年
BibTeX
@misc{reference.wolfram_2025_sphericalshell, author="Wolfram Research", title="{SphericalShell}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/SphericalShell.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_sphericalshell, organization={Wolfram Research}, title={SphericalShell}, year={2015}, url={https://reference.wolfram.com/language/ref/SphericalShell.html}, note=[Accessed: 08-January-2026]}