WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

SystemModelLinearize[model]

平衡点における model についての線形化された状態空間モデルStateSpaceModelを与える．

SystemModelLinearize[model,op]

操作点 op で線形化する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
モデルタイプ  
限定的なケース  
線形化の値  
操作点  
一般化と拡張  
オプション  
Method  
ProgressReporting  
アプリケーション  
線形化された系を解析する  
線形化された系の制御設計  
特性と関係  
考えられる問題  
関連項目
関連するガイド
関連リンク
履歴
引用書式

SystemModelLinearize

SystemModelLinearize[model]

平衡点における model についての線形化された状態空間モデルStateSpaceModelを与える．

SystemModelLinearize[model,op]

操作点 op で線形化する．

詳細とオプション

  • SystemModelLinearizeは，操作点近くにおける model の線形近似を与える．
  • 線形モデルは，制御設計，最適化，周波数解析等でよく使われる．
  • 方程式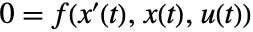と出力方程式 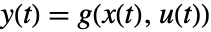を持つ系は，f(0,x0,u0)0を満足する操作点 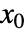および 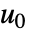で線形化される．
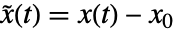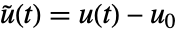  • 返される線形状態空間モデルStateSpaceModelは，状態 ，入力 ，出力 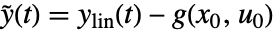を持つ．状態方程式は 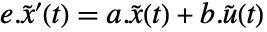で出力方程式は 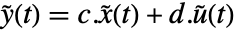である．行列は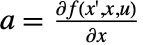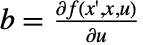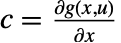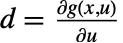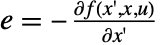，, , , , （すべてがt 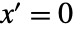, 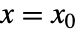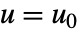，で評価される）で与えられる．
  • SystemModelLinearize[model]はSystemModelLinearize[model,"EquilibriumValues"]に等しい．
  • op の指定には，操作点として次の値が使われる．
  • "InitialValues"model からの初期値
    "EquilibriumValues"FindSystemModelEquilibrium[model]
    sim または {sim,"StopTime"} SystemModelSimulationData sim からの最終値
    {sim,"StartTime"}sim の初期値
    {sim,time}time における sim からの値
    {{{x1,x10},…},{{u1,u10},…}}状態値 xi0と入力値 ui0
  • シミュレーション sim はSystemModelSimulate[model,All,…]を使って得ることができる．
  • SystemModelLinearizeは，微分代数方程式系を記号的に線形化する．あるいは，微分代数方程式を常微分方程式系に簡約し，結果の常微分方程式系を数値的に線形化する．
  • 次は，使用可能なオプションである．
  • Method Automatic線形化アルゴリズムのメソッド
    ProgressReporting $ProgressReporting進捗状況の表示を制御する
  • オプションMethodには次の可能な設定がある．
  • "NumericDerivative"常微分方程式に簡約してから数値的に線形化する
    "SymbolicDerivative"微分代数方程式系を記号的に線形化する
  • Method{"SymbolicDerivative","ReduceIndex"False}は指数削減をオフにする．

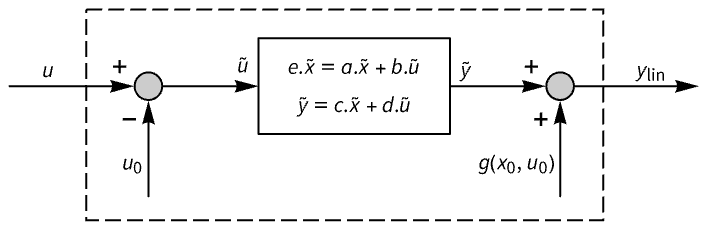
例題

すべて開く すべて閉じる

例  (3)

DCモーターモデルを平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

指定された状態と入力条件を使って，混合タンクモデルを平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], {{{"H", 0.75}}, {{"u1", 5.23}}}]

製品に含まれているintroductory hierarchicalの例の1つを線形化する：

Wolfram Language code: model = Last@SystemModelExamples["Models", "IntroductoryExamples.Hierarchical.*"]
Wolfram Language code: SystemModelLinearize[model]

スコープ  (19)

モデルタイプ  (5)

テキストのRLC回路モデルを線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

RLC回路のブロック図モデルを線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

非因果的RLC回路を線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

微分代数方程式(DAE)モデルを線形化する：

Wolfram Language code: SystemModelLinearize[\!\(\*GraphicsBox[«8»]\)]

DAEモデルを記号的に線形化する：

Wolfram Language code: SystemModelLinearize[\!\(\*GraphicsBox[«8»]\), Method -> {"SymbolicDerivative", "SymbolicParameters" -> {"R1", "R2", "L"}}]

限定的なケース  (3)

入力のないモデルを線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

状態のないモデルを線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

出力のないモデルを線形化する：

Wolfram Language code: SystemModelLinearize[[image]]

線形化の値  (5)

平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], "EquilibriumValues"]

初期値の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], "InitialValues"]

与えられた状態と入力条件で，平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], {{{"H1", 2.03}, {"T1", 318.15}, {"T2", 318.15}}, {{"u1", 5}, {"u2", 5}}}, "EquilibriumValues"]

制約条件のある状態で，平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], {{{"H1", 5}, {"T1", 318.15}, {"T2", 318.15}}, {}}, "EquilibriumValues"]

指定された部分的な状態と入力の周りで，残りの値には初期値を使って線形化する：

Wolfram Language code: SystemModelLinearize[[image], {{{"H1", 3.03}, {"T1", 318.15}, {"T2", 318.15}}, {{"u1", 5}, {"u2", 5}}}, "InitialValues"]

操作点  (6)

平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], "EquilibriumValues"]

初期値の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], "InitialValues"]

与えられた状態と入力の制約の下で，平衡点の周りで線形化する：

Wolfram Language code: SystemModelLinearize[[image], {{{"H1", 2.03}, {"T1", 318.15}, {"T2", 318.15}}, {{"u1", 5}, {"u2", 5}}}, "EquilibriumValues"]

シミュレーションからの初期値の周りで線形化する：

Wolfram Language code: sim = SystemModelSimulate[[image], All, {0, 0}]
Wolfram Language code: SystemModelLinearize[[image], {sim, "StartTime"}]

シミュレーションからの最終の値の周りで線形化する：

Wolfram Language code: sim = SystemModelSimulate[[image], All]
Wolfram Language code: SystemModelLinearize[[image], {sim, "StopTime"}]

シミュレーションの実行から定常状態までの最終の値の周りで線形化する：

Wolfram Language code: sim = SystemModelSimulate[[image], All, Method -> {"StopAtSteadyState" -> True}]
Wolfram Language code: SystemModelLinearize[[image], {sim, "StopTime"}]

一般化と拡張  (1)

結果のStateSpaceModelのラベルを隠す：

Wolfram Language code: SystemModelLinearize[[image], SystemsModelLabels -> None]

オプション  (5)

Method  (4)

"SymbolicDerivative"メソッドは，シミュレーションからの完全に指定された操作点を使う：

Wolfram Language code: sim = SystemModelSimulate[[image], All, {0, 0}]
Wolfram Language code: SystemModelLinearize[[image], sim, Method -> "SymbolicDerivative"]

"NumericDerivative"メソッドは，状態と入力の値で指定された操作点を使う：

Wolfram Language code: SystemModelLinearize[[image], {{{"capacitor.v", 0.}, {"inductor.i", 0.}}, {{"v", 0.}}}, Method -> "NumericDerivative"]

記号的に線形化することで，いくつかのパラメータを記号のままにしておける：

Wolfram Language code: SystemModelLinearize[[image], Method -> {"SymbolicDerivative", "SymbolicParameters" -> {"R", "L", "C"}}]

"ReduceIndex"を使って記号的に線形化する際に指標削減をオフにする：

Wolfram Language code: sim = SystemModelSimulate[[image], All, {0, 0}];

指標削減をオフにすると記述子のStateSpaceModelになる：

Wolfram Language code: SystemModelLinearize[[image], sim, Method -> {"SymbolicDerivative", "ReduceIndex" -> False}]

ProgressReporting  (1)

ProgressReportingで進捗状況の報告を制御する：

Wolfram Language code: SystemModelLinearize[[image], ProgressReporting -> False]

アプリケーション  (10)

線形化された系を解析する  (5)

あるモデルとその線形化されたものからの平衡点における応答を比較する：

Wolfram Language code: model = [image];
Wolfram Language code: {Subscript[x, 0], Subscript[u, 0], Subscript[y, 0]} = FindSystemModelEquilibrium[model];

平衡点の周りで線形化する：

Wolfram Language code: ss = SystemModelLinearize[model, "EquilibriumValues"];

定常出力応答を非線形モデルと比較する：

Wolfram Language code: {linY1, linY2} = OutputResponse[ss, {UnitStep[t], UnitStep[t]}, {t, 0, 300}];
Wolfram Language code: nonLin = SystemModelSimulate[model, {0, 300}, <|"InitialValues" -> Rule@@@Subscript[x, 0], "Inputs" -> {"u1" -> Function[t, Subscript[u, 0][[1, 2]] + UnitStep[t]], "u2" -> Function[t, Subscript[u, 0][[2, 2]] + UnitStep[t]]}|>];

y1出力を比較する：

Wolfram Language code: Show[SystemModelPlot[nonLin, {"y1"}], Plot[Tooltip[Subscript[y, 0][[1, 2]] + linY1, "linear y1"], {t, 0, 300}]]

系の行列の固有値から，線形化された系の安定性をテストする：

Wolfram Language code: ss = SystemModelLinearize[[image], "InitialValues"]

正の実部を持つ固有値があるので，この系は不安定である：

Wolfram Language code: {a, b, c, d} = Normal[ss];
Wolfram Language code: Re@Eigenvalues[a]

出力応答をプロットしても，この系が不安定であるのが分かる：

Wolfram Language code: Plot[Evaluate[OutputResponse[ss, UnitStep[t], {t, 1}]], {t, 0, 1}]

伝達関数の極から，線形化された系の安定性をテストする：

Wolfram Language code: tf = TransferFunctionModel@SystemModelLinearize[[image]];

正の実部を持つ極があるので，この系は不安定である：

Wolfram Language code: TransferFunctionPoles[tf]

線形モデルを使って周波数解析を行う：

Wolfram Language code: model = \!\(\*GraphicsBox[«8»]\);

線形化された伝達関数 についてのTemplateBox[{{H, (, {ⅈ, , omega}, )}}, Abs] をプロットする：

Wolfram Language code: ss = SystemModelLinearize[model];
Wolfram Language code: BodePlot[ss, {0.5, 3}, PlotLayout -> "Magnitude"]

Fourierをシミュレーションデータに使って結果を検証する：

Wolfram Language code: nonLin = SystemModelSimulate[model, {0, 200}, <|"Inputs" -> {"u" -> Function[t, UnitStep[t] - UnitStep[t - 2]]}|>];

からTemplateBox[{{H, (, {ⅈ, , omega}, )}}, Abs]を計算する：

Wolfram Language code: odata = Abs@Fourier@Table[nonLin[{"inertia3.w"}, t][[1]], {t, 0, 200, 0.25}]; idata = Abs@Fourier@Table[UnitStep[t] - UnitStep[t - 2], {t, 0, 200, 0.25}];
Wolfram Language code: ListLogLinearPlot[odata[[1 ;; 200]] / idata[[1 ;; 200]], Joined -> True, DataRange -> {0, 2Pi}, PlotRange -> {{0.5, 3}, {0, 50}}]

固有値の虚部は共振ピークを与える：

Wolfram Language code: {a, b, c, d} = Normal[ss];
Wolfram Language code: Im[Eigenvalues[a]]

線形化は時点0で行われる：

Wolfram Language code: model = [image];

時点0に接続したスイッチで線形化する：

Wolfram Language code: model2 = SystemModel[model, {"t" -> 0}];
Wolfram Language code: rlc = SystemModelLinearize[model2]

スイッチが時点0に接続されていなければ，違った結果になる：

Wolfram Language code: model3 = SystemModel[model2, {"t" -> 1}];
Wolfram Language code: rl = SystemModelLinearize[model3]

線形化された系の制御設計  (5)

線形化されたモデルを使ってPID制御を設計する：

Wolfram Language code: tf = TransferFunctionModel@SystemModelLinearize[[image]];

PID制御と閉ループ伝達関数を定義する：

Wolfram Language code: pidTf = TransferFunctionModel[kp (1 + 1 / (τi ) + τd ), ];
Wolfram Language code: cltf = SystemsModelFeedbackConnect[SystemsModelSeriesConnect[pidTf, tf]];

適切なステップ応答のためにPIDパラメータを選択する：

Wolfram Language code: Manipulate[ Plot[OutputResponse[cltf /. {kp -> gain, τi -> iTime, τd -> dTime}, UnitStep[t], {t, 20}]//Evaluate, {t, 0, 20}, PlotStyle -> Thick, GridLines -> Automatic, Frame -> True, PlotRange -> {0, 1.2}], {{gain, 1, "SubscriptBox[k, p]"}, 0.01, 10}, {{dTime, 0.01, "SubscriptBox[τ, d]"}, 0.01, 10}, {{iTime, 1.9, "SubscriptBox[τ, i]"}, 0.01, 10}, SaveDefinitions -> True]

DCモーターのためのleadベースの制御を，モーターの線形化に基づいて設計する：

Wolfram Language code: tf = TransferFunctionModel@SystemModelLinearize[[image]];

PI-lead制御伝達関数を定義する：

Wolfram Language code: piLeadTf = TransferFunctionModel[kp (1 + 1 / τi (τd  + 1) / (α τd  + 1)), ];

開ループ伝達関数：

Wolfram Language code: optf = SystemsModelSeriesConnect[piLeadTf, tf];

制御のパラメータを選ぶ：

Wolfram Language code: Manipulate[BodePlot[newOptf = optf /. {kp -> Kp, τi -> Τi, τd -> Τd, α -> Α}, StabilityMargins -> True, PlotLayout -> "List"], {{Kp, 4.5, "SubscriptBox[k, p]"}, 0.01, 10}, {{Τi, 2, "τi"}, 0.01, 10}, {{Τd, 0.01, "τd"}, 0.01, 10}, {{Α, 0.07, "α"}, 0.01, 0.9}, SaveDefinitions -> True]

選択されたパラメータを使い，PI-lead制御でループを閉じる：

Wolfram Language code: cltf = SystemsModelFeedbackConnect[SystemsModelSeriesConnect[newOptf, tf]];
Wolfram Language code: Plot[OutputResponse[cltf, UnitStep[t], {t, 20}]//Evaluate, {t, 0, 20}, PlotStyle -> Thick, GridLines -> Automatic, Frame -> True, PlotRange -> All]

極配置を使って制御を設計する：

Wolfram Language code: ss = SystemModelLinearize[[image]];

閉ループ極を置く：

Wolfram Language code: k = StateFeedbackGains[ss, {-0.251, -0.222, -0.222}]

閉ループ状態空間モデルを計算する：

Wolfram Language code: clss = SystemsModelStateFeedbackConnect[ss, k];

ステップ応答を表示する：

Wolfram Language code: Plot[OutputResponse[clss, {UnitStep[t], UnitStep[t]}, {t, 100}]//Evaluate, {t, 0, 100}, PlotRange -> All]

LQ制御を設計する：

Wolfram Language code: ss = SystemModelLinearize[[image]];

状態と入力の重み行列を定義する：

Wolfram Language code: {q1, q2} = {DiagonalMatrix[{1, 6 10^-4, 6 10^-4}], DiagonalMatrix[{0.0002, 0.0002}]};

LQ制御ゲインを定義する：

Wolfram Language code: k = LQRegulatorGains[ss, {q1, q2}]

閉ループ状態空間モデル：

Wolfram Language code: clss = SystemsModelStateFeedbackConnect[ss, k];

閉ループステップ応答：

Wolfram Language code: Plot[OutputResponse[clss, {UnitStep[t], UnitStep[t]}, {t, 100}]//Evaluate, {t, 0, 100}, PlotRange -> All]

状態推定器を設計する：

Wolfram Language code: model = [image];
Wolfram Language code: ss = SystemModelLinearize[model];

推定器ゲインと推定器状態空間モデルを計算する：

Wolfram Language code: l = EstimatorGains[ss, {-0.6020, -0.5856, -0.5697}]
Wolfram Language code: {a, b, c, d} = Normal[ss];
Wolfram Language code: ssobsv = StateSpaceModel[{a - l.c, ArrayFlatten[{{b - l.d, l}}], IdentityMatrix[3]}];

この入力の単位ステップについての状態と出力応答：

Wolfram Language code: sresp = StateResponse[ss, {UnitStep[t], UnitStep[t]}, {t, 200}];
Wolfram Language code: y = OutputResponse[ss, {UnitStep[t], UnitStep[t]}, {t, 200}];

観察者の状態応答：

Wolfram Language code: oresp = OutputResponse[ssobsv, {UnitStep[t], UnitStep[t], y[[1]], y[[2]]}, {t, 200}];

各状態をその推定と比較する：

Wolfram Language code: states = model["StateVariables"];
Wolfram Language code: Table[Plot[{sresp[[i]], oresp[[i]]}, {t, 0, 200}, PlotLabel -> states[[i]]], {i, 3}]

特性と関係  (8)

SystemModelからのプロパティを使って初期値の周りで線形化する：

Wolfram Language code: model = [image];
Wolfram Language code: ival = model["GroupedInitialValues"]

結果を比較する：

Wolfram Language code: SystemModelLinearize[model, ival, "InitialValues"] == SystemModelLinearize[model, "InitialValues"]

FindSystemModelEquilibriumを使って平衡点の周りで線形化する：

Wolfram Language code: model = [image];
Wolfram Language code: eqval = FindSystemModelEquilibrium[model];

結果を比較する：

Wolfram Language code: SystemModelLinearize[model, eqval] == SystemModelLinearize[model, "EquilibriumValues"]


モデルと平衡点におけるその線形化からの応答を比較する：

Wolfram Language code: model = [image];
Wolfram Language code: {Subscript[x, 0], Subscript[u, 0], Subscript[y, 0]} = FindSystemModelEquilibrium[model, {"H" == 0.85, "Tu" == 38, "Tx" == 38}]

平衡点の周りで線形化する：

Wolfram Language code: ss = SystemModelLinearize[model, {{{"H", 0.85}, {"Tu", 38}, {"Tx", 38}}, {}}, "EquilibriumValues"]

定常出力応答を非線形モデルと比較する：

Wolfram Language code: {linY1, linY2} = OutputResponse[ss, {UnitStep[t], UnitStep[t]}, {t, 0, 300}];
Wolfram Language code: nonLin = SystemModelSimulate[model, {0, 300}, <|"InitialValues" -> Rule@@@Subscript[x, 0], "Inputs" -> {"u1" -> Function[t, Subscript[u, 0][[1, 2]] + UnitStep[t]], "u2" -> Function[t, Subscript[u, 0][[2, 2]] + UnitStep[t]]}|>];

最初の出力を比較する：

Wolfram Language code: Show[SystemModelPlot[nonLin, {"y1"}], Plot[Evaluate@Tooltip[Subscript[y, 0][[1, 2]] + linY1, "linear y1"], {t, 0, 300}]]

モデルと非平衡点におけるその線形化からの応答を比較する：

Wolfram Language code: model = [image];
Wolfram Language code: Subscript[x, 0] = {{"H", 0.85}, {"Tu", 38}, {"Tx", 38}}
Wolfram Language code: Subscript[u, 0] = {{"u1", 5.23}, {"u2", 3.08}}

指定された点の周りで線形化する：

Wolfram Language code: ss = SystemModelLinearize[model, {Subscript[x, 0], Subscript[u, 0]}, "InitialValues"];

定常出力応答を非線形モデルと比較する：

Wolfram Language code: {linY1, linY2} = OutputResponse[ss, {UnitStep[t], UnitStep[t]}, {t, 0, 300}];
Wolfram Language code: nonLin = SystemModelSimulate[model, {0, 300}, <|"InitialValues" -> Rule@@@Subscript[x, 0], "Inputs" -> {"u1" -> Function[t, Subscript[u, 0][[1, 2]] + UnitStep[t]], "u2" -> Function[t, Subscript[u, 0][[2, 2]] + UnitStep[t]]}|>];

出力方程式を得る：

Wolfram Language code: eqs = model["SystemEquations", t] /. model["ParameterValues"]
Wolfram Language code: Subscript[g, out] = Cases[eqs, (QuantityVariable["y1", _] | QuantityVariable["y2", _])[t] == rhs__ :> rhs];

定常出力を計算する：

Wolfram Language code: {Subscript[y, 2, 0], Subscript[y, 1, 0]} = Subscript[g, out] /. (Function[{var, val}, QuantityVariable[var, _][t] -> val]@@@Subscript[x, 0]);

最初の出力を比較する：

Wolfram Language code: Show[Plot[Evaluate@Tooltip[Subscript[y, 1, 0] + linY1, "linear y1"], {t, 0, 300}], SystemModelPlot[nonLin, {"y1"}]]

TransferFunctionModelを使って伝達関数表現に変換する：

Wolfram Language code: SystemModelLinearize[[image]]
Wolfram Language code: TransferFunctionModel[%]

ToDiscreteTimeModelを使って線形モデルを離散化する：

Wolfram Language code: SystemModelLinearize[[image]]

サンプル時間0.10を使って離散化する：

Wolfram Language code: ToDiscreteTimeModel[%, 0.10, z]

線形化された状態空間モデルは一意的ではない：

Wolfram Language code: linearize1 = [image];
Wolfram Language code: linearize1["ModelicaDisplay"]
Wolfram Language code: ss1 = SystemModelLinearize[linearize1]

変数x1とx2が宣言された順序を変える：

Wolfram Language code: linearize2 = [image];
Wolfram Language code: linearize2["ModelicaDisplay"]
Wolfram Language code: ss2 = SystemModelLinearize[linearize2]

両モデルは等価であり，同一の伝達関数を持つ：

Wolfram Language code: TransferFunctionModel[ss1] == TransferFunctionModel[ss2]

StateSpaceModelは常微分方程式系を線形化できる：

Wolfram Language code: ClearAll[t, x, θ, i, vin, g, r, lin, mc, mp, l, k, dc, dp, a];
Wolfram Language code: eqs = {(mc + mp)x''[t] - mp l Cos[θ[t]] θ''[t] + mp l Sin[θ[t]] θ'[t]^2 == k i[t] - dc x'[t], θ''[t]mp (4l^2 / 3 + a^2 / 4) - mp l x''[t] Cos[θ[t]] == mp g l Sin[θ[t]] - dp θ'[t], 0 == vin[t] - r i[t] - lin i'[t] - k x'[t]};
Wolfram Language code: opssm = Sequence[{{i[t], 0}, {θ[t], 0}, {θ'[t], 0}, {x[t], 0}, {x'[t], 0}}, {{vin[t], 0}}];
Wolfram Language code: outputs = {θ[t], x[t]};
Wolfram Language code: ssm = StateSpaceModel[eqs, opssm, outputs, t]//Simplify

近似数値パラメータ値を使う：

Wolfram Language code: parVals = {g -> 9.80665, r -> 13, lin -> 1, mc -> 445 * 0.1^3, mp -> 7700 * π * 0.005^2 * 0.61, l -> 0.61 / 2, a -> 0.005, k -> 3.7 * 157.48 * 1.6, dc -> 2, dp -> 0.01};
Wolfram Language code: ssm /. parVals

SystemModelLinearizeを使って同じ系のSystemModelを線形化する：

Wolfram Language code: model = SystemModel[[image], <|"ParameterValues" -> {"electricalMotor.J" -> 0}|>];
Wolfram Language code: op = FindSystemModelEquilibrium[model]
Wolfram Language code: SystemModelLinearize[model, op]

方程式からNonlinearStateSpaceModelを作成し，SystemModelと比較する：

Wolfram Language code: nssm = NonlinearStateSpaceModel[eqs, opssm, outputs, t]//Simplify
Wolfram Language code: plotComparison[nssmVar_, smVar_] := Show[SystemModelPlot[nssm, {nssmVar}, 20, <|"ParameterValues" -> parVals, "Inputs" -> {vin -> UnitBox}|>, PlotLabel -> nssmVar, ...], SystemModelPlot[model, {smVar}, 20, <|"Inputs" -> {"V" -> UnitBox}|>, TargetUnits -> "Unit", ...]];
Wolfram Language code: plotComparison[θ, "pendulum.pendulumDamper.phi_rel"]
Wolfram Language code: plotComparison[x, "pendulum.sliderConstraint.s"]

考えられる問題  (1)

モデルの中には記号的には線形化できないものがある：

Wolfram Language code: SystemModelLinearize["DocumentationExamples.Modeling.ElectricCircuit.CircuitWithEvent", Method -> "SymbolicDerivative"]
Wolfram Language code: SystemModelLinearize["DocumentationExamples.Basic.StateOut", Method -> "SymbolicDerivative"]
Wolfram Language code: SystemModelLinearize["DocumentationExamples.Basic.InOutNoState", Method -> "SymbolicDerivative"]

"NumericDerivative"を使って数値的に線形化する：

Wolfram Language code: SystemModelLinearize["DocumentationExamples.Modeling.ElectricCircuit.CircuitWithEvent", Method -> "NumericDerivative"]
Wolfram Research (2018), SystemModelLinearize, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemModelLinearize.html （2020年に更新）.

テキスト

Wolfram Research (2018), SystemModelLinearize, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemModelLinearize.html （2020年に更新）.

CMS

Wolfram Language. 2018. "SystemModelLinearize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/SystemModelLinearize.html.

APA

Wolfram Language. (2018). SystemModelLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelLinearize.html

BibTeX

@misc{reference.wolfram_2026_systemmodellinearize, author="Wolfram Research", title="{SystemModelLinearize}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelLinearize.html}", note=[Accessed: 01-September-2026]}

BibLaTeX

@online{reference.wolfram_2026_systemmodellinearize, organization={Wolfram Research}, title={SystemModelLinearize}, year={2020}, url={https://reference.wolfram.com/language/ref/SystemModelLinearize.html}, note=[Accessed: 01-September-2026]}