SystemModelLinearize[model]
gives a linearized StateSpaceModel for model at an equilibrium.
SystemModelLinearize[model,op]
linearizes at the operating point op.


SystemModelLinearize
SystemModelLinearize[model]
gives a linearized StateSpaceModel for model at an equilibrium.
SystemModelLinearize[model,op]
linearizes at the operating point op.
Details and Options


- SystemModelLinearize gives a linear approximation of model near an operating point.
- A linear model is typically used for control design, optimization and frequency analysis.
- A system with equations
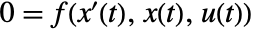 and output equations
and output equations 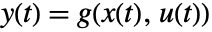 is linearized at an operating point
is linearized at an operating point 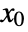 and
and 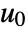 that should satisfy f(0,x0,u0)0.
that should satisfy f(0,x0,u0)0. - The returned linear StateSpaceModel has state
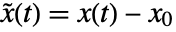 , input
, input 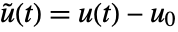 and output
and output 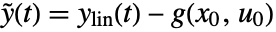 , with state equations
, with state equations 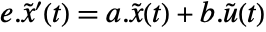 and output equation
and output equation 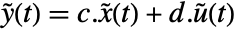 . The matrices are given by
. The matrices are given by 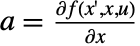 ,
, 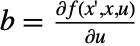 ,
, 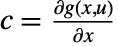 ,
, 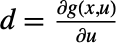 and
and 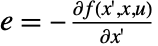 , all evaluated at
, all evaluated at 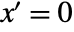 ,
, 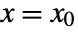 and
and 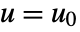 .
. - SystemModelLinearize[model] is equivalent to SystemModelLinearize[model,"EquilibriumValues"].
- Specifications for op use the following values for the operating point:
-
"InitialValues" initial values from model "EquilibriumValues" FindSystemModelEquilibrium[model] sim or {sim,"StopTime"} final values from SystemModelSimulationData sim {sim,"StartTime"} initial values of sim {sim,time} values at time from sim {{{x1,x10},…},{{u1,u10},…}} state values xi0 and input values ui0 - The simulation sim can be obtained using SystemModelSimulate[model,All,…].
- SystemModelLinearize linearizes a system of DAEs symbolically, or first reduces it to a system of ODEs and linearizes the resulting ODEs numerically.
- The following options can be given:
-
Method Automatic methods for linearization algorithm ProgressReporting $ProgressReporting control display of progress - The option Method has the following possible settings:
-
"NumericDerivative" reduces to ODEs and then linearizes numerically "SymbolicDerivative" linearizes symbolically from a system of DAEs - Method{"SymbolicDerivative","ReduceIndex"False} turns off index reduction.
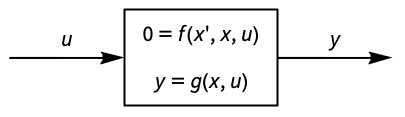
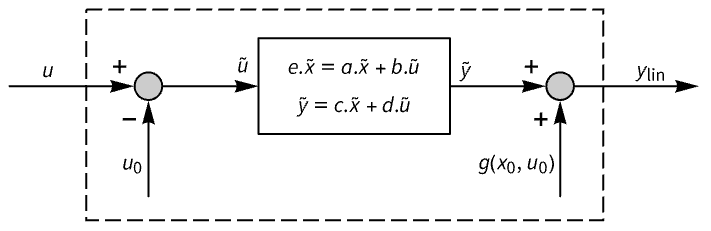
Examples
open all close allBasic Examples (3)
Linearize a DC-motor model around an equilibrium:
Linearize a mixing tank model around equilibrium with given state and input constraints:
Linearize one of the included introductory hierarchical examples:
Scope (19)
Model Types (5)
Limiting Cases (3)
Linearization Values (5)
Operating Point (6)
Linearize around an equilibrium:
Linearize around initial values:
Linearize around equilibrium with given state and input constraints:
Linearize around initial values from a simulation:
Linearize around final values from a simulation:
Linearize around final values from a simulation run to steady state:
Generalizations & Extensions (1)
Hide labels in the resulting StateSpaceModel:
Options (5)
Method (4)
The "SymbolicDerivative" method uses a fully specified operating point from a simulation:
The "NumericDerivative" method uses an operating point specified by state and input values:
Linearizing symbolically allows keeping some parameters symbolic:
Use "ReduceIndex" to turn off index reduction when linearizing symbolically:
Turning off index reduction results in a descriptor StateSpaceModel:
ProgressReporting (1)
Control progress reporting with ProgressReporting:
Applications (10)
Analyzing Linearized System (5)
Compare responses from a model and its linearization at an equilibrium point:
Linearize around the equilibrium point:
Compare the stationary output response with a nonlinear model:
Test the stability of a linearized system from eigenvalues of the system matrix:
Since there is an eigenvalue with a positive real part, the system is unstable:
Plotting the output response also indicates an unstable system:
Test the stability of a linearized system from poles of the transfer function:
Since there is a pole with a positive real part, the system is unstable:
Do a frequency analysis using a linear model:
By plotting ![]() for the linearized transfer function
for the linearized transfer function ![]() :
:
Verify the result using Fourier on simulated data:
Alternatively, the imaginary parts of the eigenvalues give the resonance peaks:
Linearization takes place at time 0:
Linearize with the switch connecting at time 0:
If the switch is not connected at time 0, the result is different:
Controller Design for Linearized System (5)
Design a PID controller using a linearized model:
Define a PID controller and closed-loop transfer function:
Select PID parameters for appropriate step response:
Design a lead-based controller for a DC motor based on its linearization:
Define a PI-lead controller transfer function:
Use selected parameters and close the loop with the PI-lead controller:
Design a controller using pole placement:
Compute the closed-loop state-space model:
Define state and input weight matrices:
Closed-loop state-space model:
Compute estimator gains and the estimator state-space model:
Properties & Relations (8)
Linearize around initial values using properties from SystemModel:
Linearize around equilibrium using FindSystemModelEquilibrium:
Compare responses from a model and its linearization at an equilibrium point:
Linearize around the equilibrium point:
Compare the stationary output response with a nonlinear model:
Compare responses from a model and its linearization at a non-equilibrium point:
Linearize around the given point:
Compare the stationary output response with a nonlinear model:
Compute the stationary output:
Use TransferFunctionModel to convert to a transfer function representation:
Use ToDiscreteTimeModel to discretize a linearized model:
Discretize using sample time ![]() :
:
The linearized state-space model is not unique:
Change the order in which the variables x1 and x2 are declared:
The models are equivalent and have identical transfer functions:
StateSpaceModel can linearize systems of ordinary differential equations:
Use approximate numeric parameter values:
Use SystemModelLinearize to linearize a SystemModel of the same system:
Create a NonlinearStateSpaceModel from the equations and compare with the SystemModel:
Related Guides
Related Links
Text
Wolfram Research (2018), SystemModelLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemModelLinearize.html (updated 2020).
CMS
Wolfram Language. 2018. "SystemModelLinearize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/SystemModelLinearize.html.
APA
Wolfram Language. (2018). SystemModelLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemModelLinearize.html
BibTeX
@misc{reference.wolfram_2025_systemmodellinearize, author="Wolfram Research", title="{SystemModelLinearize}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelLinearize.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemmodellinearize, organization={Wolfram Research}, title={SystemModelLinearize}, year={2020}, url={https://reference.wolfram.com/language/ref/SystemModelLinearize.html}, note=[Accessed: 06-January-2026]}

