SystemsModelDelay

SystemsModelDelay[δ]

represents a time delay of δ in a StateSpaceModel or TransferFunctionModel.

Details

  • SystemsModelDelay[δ] makes it possible to represent systems involving time delays and efficiently manipulate, approximate, and simulate these systems.
  • SystemsModelDelay[δ] is typeset in StandardForm as δ and can be entered using delay.
  • For a StateSpaceModel, SystemsModelDelay[δ] can occur linearly in any of the system matrices. For a signal 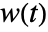, SystemsModelDelay[δ]w[t] is taken to be .
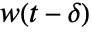  • For a TransferFunctionModel, SystemsModelDelay[δ] can occur linearly in the coefficients of the polynomials. It is taken to represent a transformed time delay:
  • -δ sin a continuous-time system
    z-δin a discrete-time system
  • Here, s is the Laplace-transform variable, and z is the z-transform variable.
  • For discrete-time systems, the delay δ is taken to be a multiple of the SamplingPeriod.

Examples

open allclose all

Basic Examples  (3)

A state-space model with an input delay:

A transfer-function model with delay:

A time-delay state-space model created from delay differential equations:

Scope  (7)

A continuous-time state-space model with a state delay:

A discrete-time state-space model with an output delay:

A continuous-time transfer-function model with delay:

Or represent the delay as an exponential:

A discrete-time transfer-function model with delay:

A state-space model with a delay in the descriptor matrix:

A continuous-time state-space model created from delay differential equations:

A discrete-time system from a difference equation including SystemsModelDelay:

Applications  (1)

The delay differential equation below describes the motion of the cutting tool in a lathe where the force on the tool depends on the position of the tool from the previous rotation:

The delay creates peaks in the frequency response:

Properties & Relations  (5)

A zero delay reduces to 1:

Delays in continuous-time transfer functions are equivalent to exponentials:

Delays in discrete-time transfer-function models are equivalent to additional poles:

State-space systems with neutral delays have delays in the descriptor matrix:

When converting to a transfer function, state delays appear in the denominator:

Possible Issues  (1)

In discrete-time systems, delays should have integer values:

When necessary, zero-order approximations are used:

Approximating delays before simulation can give a more accurate result:

Wolfram Research (2012), SystemsModelDelay, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelDelay.html.

Text

Wolfram Research (2012), SystemsModelDelay, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelDelay.html.

CMS

Wolfram Language. 2012. "SystemsModelDelay." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelDelay.html.

APA

Wolfram Language. (2012). SystemsModelDelay. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelDelay.html

BibTeX

@misc{reference.wolfram_2024_systemsmodeldelay, author="Wolfram Research", title="{SystemsModelDelay}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelDelay.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_systemsmodeldelay, organization={Wolfram Research}, title={SystemsModelDelay}, year={2012}, url={https://reference.wolfram.com/language/ref/SystemsModelDelay.html}, note=[Accessed: 21-December-2024 ]}