SystemsModelVectorRelativeOrders[sys]
gives the vector-relative orders of the systems model sys.


SystemsModelVectorRelativeOrders
SystemsModelVectorRelativeOrders[sys]
gives the vector-relative orders of the systems model sys.
Details and Options

- SystemsModelVectorRelativeOrders is also known as vector-relative degrees.
- The relative order of an output
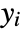 of sys is essentially the number of times it must be differentiated for the input
of sys is essentially the number of times it must be differentiated for the input 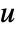 of sys to appear explicitly.
of sys to appear explicitly. - Output
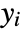 has relative order
has relative order 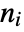 if after
if after 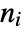 differentiations of the output,
differentiations of the output, 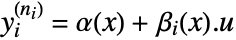 .
. - The vector-relative orders are the list of the relative orders
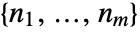 for each output.
for each output. - The matrix
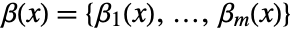 is called the decoupling matrix and needs to have rank
is called the decoupling matrix and needs to have rank 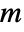 .
. - The system sys can be a TransferFunctionModel, StateSpaceModel, or AffineStateSpaceModel.
- The following options can be given:
-
MaxIterations Automatic maximum number of differentiations ZeroTest Automatic zero test
Examples
open all close allScope (4)
The vector-relative order of a single-output system:
The vector-relative orders of a multiple-output system:
The vector-relative orders of a StateSpaceModel:
The vector-relative order of a TransferFunctionModel:
Applications (2)
Determine the number of states in the feedback-linearized and residual system:
The number of states in the linear subsystem:
Feedback linearize the system:
The number of states in the residual subsystem:
In AsymptoticOutputTracker, the decay rates are assigned based on relative orders:
The first three poles correspond to the first output and the last two to the second:
The first output has slower decay rates and hence takes longer to start following the reference input:
Properties & Relations (7)
The length of the vector-relative orders is equal to the number of outputs:
Use SystemsModelDimensions to get the number of outputs:
For scalar systems with no zero dynamics, the vector-relative order equals the order:
Use SystemsModelOrder to get the order of the system:
If the vector-relative orders are finite, a linearizing feedback control can be computed:
Use FeedbackLinearize to compute the linearizing feedback:
If the sum of vector-relative orders is equal to the order, there are no zero dynamics:
The relative orders give the lengths of the integrator chains of the feedback-linearized system:
Output 1 has a single integrator and output 2 has a double integrator:
The vector-relative orders are invariant wrt a coordinate transform:
The vector-relative orders correspond to the asymptotic orders of the transfer functions:
Output 1 (first row) has asymptotic order 3, and output 2 (second row) has asymptotic order 2:
Possible Issues (3)
For the decoupling matrix to be invertible, the outputs must be independent:
There must be at least as many inputs as outputs:
If an operating point is specified, the decoupling matrix is evaluated at that point:
Although the system is feedback linearizable, there is a singularity at the operating point:
Related Guides
History
Text
Wolfram Research (2014), SystemsModelVectorRelativeOrders, Wolfram Language function, https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.
CMS
Wolfram Language. 2014. "SystemsModelVectorRelativeOrders." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html.
APA
Wolfram Language. (2014). SystemsModelVectorRelativeOrders. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html
BibTeX
@misc{reference.wolfram_2025_systemsmodelvectorrelativeorders, author="Wolfram Research", title="{SystemsModelVectorRelativeOrders}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemsmodelvectorrelativeorders, organization={Wolfram Research}, title={SystemsModelVectorRelativeOrders}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelVectorRelativeOrders.html}, note=[Accessed: 06-January-2026]}