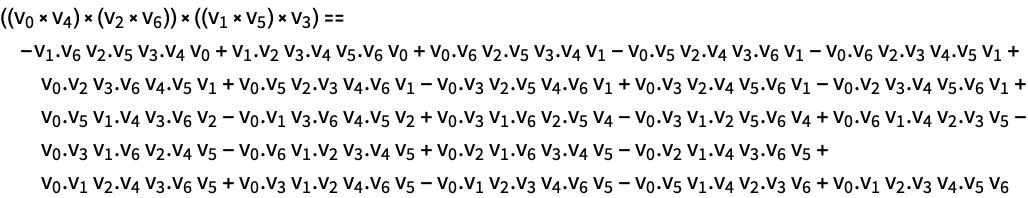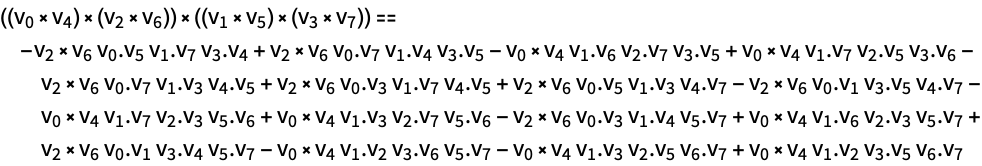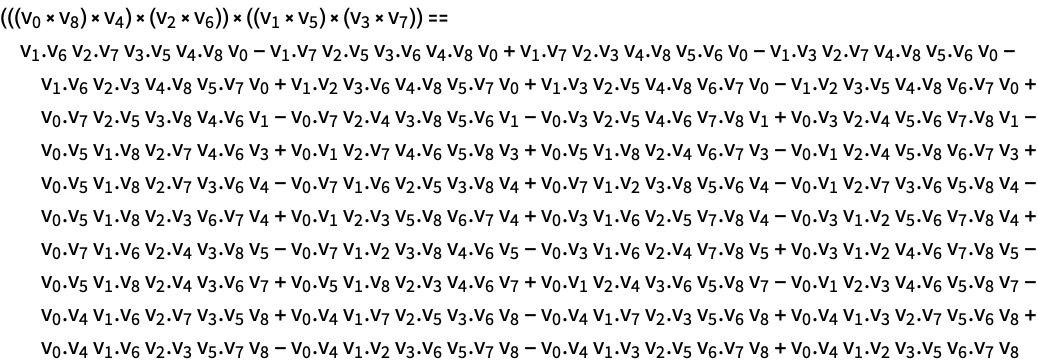TensorExpand
TensorExpand[texpr]
expands out tensor-related products in the symbolic tensor expression texpr.
Details and Options
- TensorExpand expands sums and products by scalars in tensorial arguments.
- Expressions involving Dot and Cross are expanded by converting products of pairs of Cross subexpressions into linear combinations of Dot products.
- Symbolic arguments of Cross are assumed to represent vectors of adequate dimensionality.
- Symbolic arguments of MatrixPower and Inverse are assumed to represent invertible square matrices.
Examples
open allclose allBasic Examples (2)
Scope (3)
Act on expressions containing all kinds of products:
Act on expressions containing both symbolic and explicit objects:
For some operations, additional information needs to be supplied. The Dot product is not commutative in general:
However, if the objects are declared as vectors, then it is commutative:
Options (1)
Applications (6)
Possible Issues (2)
Neat Examples (1)
For each integer n, there is a tree expression involving n Cross operations for n+1 vectors v0,…,vn:
Now systematically convert all possible combinations of cross products into dot products and one cross product:
Text
Wolfram Research (2012), TensorExpand, Wolfram Language function, https://reference.wolfram.com/language/ref/TensorExpand.html.
CMS
Wolfram Language. 2012. "TensorExpand." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TensorExpand.html.
APA
Wolfram Language. (2012). TensorExpand. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TensorExpand.html