TriangulateMesh

TriangulateMesh[mr]

生成网格区域 mr 的三角分割.

更多信息和选项

  • TriangulateMesh 亦称为三角分割、四面体网格剖分、单纯形分解、网格生成和网格细化.
  • 通常用来将区域划分为对于某些标准为最优的线 (1D)、三角形 (2D) 或四面体 (3D).
  • TriangulateMesh 有和 MeshRegion 一样的选项，更多选项和不同之处如下所示：
  • MaxCellMeasure Automatic最大单元格量度
    MeshQualityGoal Automatic每个网格单元的质量目标
    MeshRefinementFunction None若一个网格单元需细化则返回 True 的函数
    MethodAutomatic使用的方法
    PerformanceGoal$PerformanceGoal选择考虑速度还是质量
  • Method 选项的可能的设置包括：
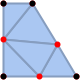
  • "ConformingDelaunay"满足 Delaunay 条件的三角分割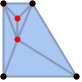
    "ConstrainedDelaunay"保留原始一维边界单元并几乎满足 Delaunay 条件的三角分割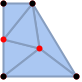
    "ConstrainedQuality"添加较少 0D 单元并几乎满足 Delaunay 条件的三角分割
  • 如果没有 mr 边界上的原始点位于 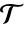中任何单纯形的外接球内，则网格 mr 的三角分割 满足 Delaunay 条件.

范例

打开所有单元关闭所有单元

基本范例  (3)

三角剖分一个在一维的 BoundaryMeshRegion：

用选项控制单元格质量和尺寸：

三角剖分一个在二维的 BoundaryMeshRegion：

用选项控制单元格质量和尺寸：

三角剖分一个三维的 BoundaryMeshRegion：

用选项控制单元格质量和尺寸：

范围  (4)

三角剖分一个在一维的 BoundaryMeshRegion：

在二维：

在三维：

三角剖分一个在一维的 MeshRegion：

在二维：

在三维：

TriangulateMesh 对维度分量单独处理：

MaxCellMeasure 控制一个单元格在三角剖分中的最大尺寸：

所使用的量度为弧长（一维网格），面积（二维网格），和体积（三维网格）：

选项  (28)

MaxCellMeasure  (6)

为一维区域设置不同的长度约束：

为二维区域设置不同的面积约束：

不同三角形的面积：

为二维区域设置边长约束：

不同边的长度：

为一个三维区域设置体积约束：

不同四面体的体积：

为一个三维区域设置面的面积约束：

不同面的面积：

为一个三维区域设置边长约束：

不同边的长度：

MeshCellHighlight  (3)

MeshCellHighlight 允许指定加亮 TriangulateMesh 的一部分：

通过让表面透明，三维 MeshRegion 的内部结构可见：

可以通过其单元索引指定加亮个别单元：

或者通过单元自己：

MeshCellLabel  (3)

MeshCellLabel 可以用于标记 TriangulateMesh 的一部分：

标记一个多边形的顶点和边：

个别单元可以通过其单元索引来标记：

或通过单元自己：

MeshCellMarker  (1)

MeshCellMarker 可用于指定 TriangulateMesh 的一部分的值：

用 MeshCellLabel 来显示标记：

MeshCellShapeFunction  (2)

MeshCellShapeFunction 允许指定 TriangulateMesh 的一部分的函数：

个别单元可以通过其单元索引画出：

或通过单元自己：

MeshCellStyle  (3)

MeshCellStyle 允许指定 TriangulateMesh 的一部分的样式：

通过是使表面透明，三维 MeshRegion 的内部结构可见：

个别单元可以通过其单元索引来加亮：

或者通过单元自己：

MeshQualityGoal  (4)

默认的设置是 Automatic：

生成一个 "Minimal" 质量的三角剖分：

生成一个 "Maximal" 质量的三角剖分：

显式设置一个量化的质量目标：

MeshRefinementFunction  (4)

用 MeshRefinementFunction 使原点左边的边变小：

用 MeshRefinementFunction 使第一象限的三角形变小：

设置一个连续变变化的面积约束：

在第一象限更细地离散化该区域：

PlotTheme  (2)

使用一个有网格线的主题和图例：

使用一个主题来画出线框：

应用  (4)

三角剖分一个多边形：

一个最小三角剖分：

三角剖分基本三维图元：

最小三角剖分：

在摩纳哥边界内进行三角剖分：

用最小数目的三角形进行三角剖分：

最大面积不超过 的三角剖分：

一个区域的非线性变换，可以近似为顶点变换：

由于网格中只有几个顶点，变换的近似效果不佳：

通过三角变换，可获得一个更准确的近似：

属性和关系  (2)

TriangulateMesh 的输出总是一个 MeshRegion：

TriangulateMesh 输出中的单元格总是为单纯形：

单纯形在二维为三角形：

Wolfram Research (2014)，TriangulateMesh，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TriangulateMesh.html （更新于 2020 年）.

文本

Wolfram Research (2014)，TriangulateMesh，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TriangulateMesh.html （更新于 2020 年）.

CMS

Wolfram 语言. 2014. "TriangulateMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/TriangulateMesh.html.

APA

Wolfram 语言. (2014). TriangulateMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TriangulateMesh.html 年

BibTeX

@misc{reference.wolfram_2024_triangulatemesh, author="Wolfram Research", title="{TriangulateMesh}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/TriangulateMesh.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_triangulatemesh, organization={Wolfram Research}, title={TriangulateMesh}, year={2020}, url={https://reference.wolfram.com/language/ref/TriangulateMesh.html}, note=[Accessed: 21-November-2024 ]}